Relativity and Black Holes
Black Holes
Next, let's solve the field equations for a spherically symmetric nonrotating
mass M at rest at the origin of a coordinate system. The solution to this
boundary value problem will tell us everything we need to know about the
dynamics of a nonrotating, uncharged black hole.
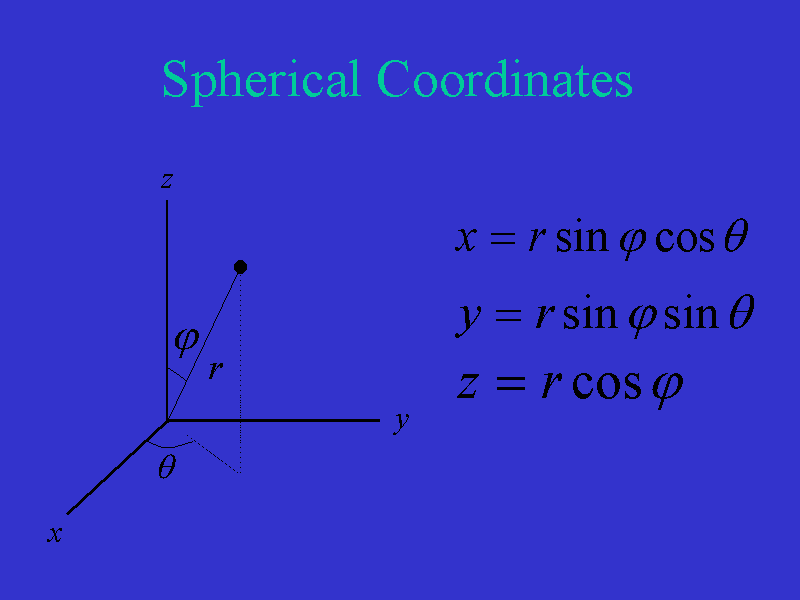 Due to the high level of symmetry with which we are dealing, we will formulate
the current problem in spherical coordinates
Due to the high level of symmetry with which we are dealing, we will formulate
the current problem in spherical coordinates  . Here we see
the relationships between rectangular coordinates
(x,y,z) and spherical
coordinates
. Here we see
the relationships between rectangular coordinates
(x,y,z) and spherical
coordinates  .
The relationship between rectangular and spherical coordinates are as
given.
.
The relationship between rectangular and spherical coordinates are as
given.
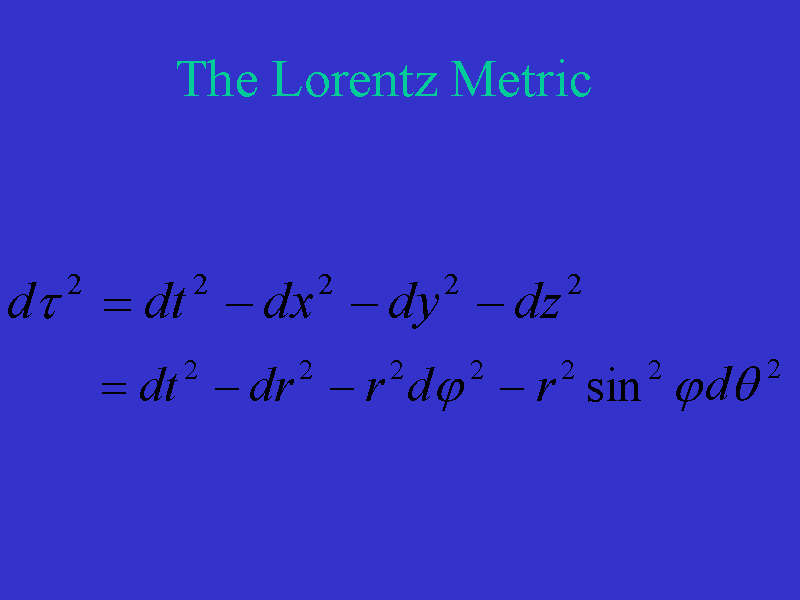 In flat spacetime, the Lorentz metric in spherical coordinates is
In flat spacetime, the Lorentz metric in spherical coordinates is
 We can verify this simply by computing the differentials of dt,
dx, dy,
dz and substituting into the expression for
We can verify this simply by computing the differentials of dt,
dx, dy,
dz and substituting into the expression for
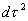 as expressed in
rectangular coordinates.
as expressed in
rectangular coordinates.
 Explicitly, the question we are addressing is this: "In the presence of a
spherically symmetric mass M at the origin of a system of spherical
coordinates, what do the field equations dictate that the metric coefficients
would be? That is, what are the gij's in the equation
Explicitly, the question we are addressing is this: "In the presence of a
spherically symmetric mass M at the origin of a system of spherical
coordinates, what do the field equations dictate that the metric coefficients
would be? That is, what are the gij's in the equation
 where we take
where we take 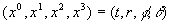 ."
Notice that we have assumed a static situation. That is, a time
independent situation.
."
Notice that we have assumed a static situation. That is, a time
independent situation.
 Therefore, our values of
the gij's will only depend on r and M.
In 1916, Karl Schwarzschild
presented the solution to this problem. His solution is
Therefore, our values of
the gij's will only depend on r and M.
In 1916, Karl Schwarzschild
presented the solution to this problem. His solution is
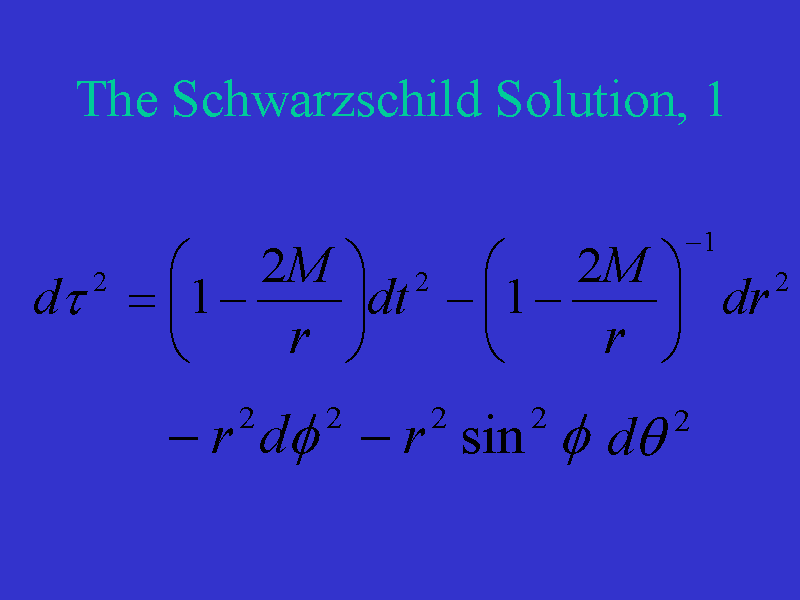 More explicitly, Schwarzschild's solution to the field equations
More explicitly, Schwarzschild's solution to the field equations
 in terms of the metric coefficients is as
seen here.
The field equations as stated earlier are only valid outside of the
relevant massive object.
in terms of the metric coefficients is as
seen here.
The field equations as stated earlier are only valid outside of the
relevant massive object.
 If we let rB denote the radius of the spherically symmetric mass, then
the Schwarzschild solution is only valid for r >
rB. Also, we see that the
metric coefficient
If we let rB denote the radius of the spherically symmetric mass, then
the Schwarzschild solution is only valid for r >
rB. Also, we see that the
metric coefficient 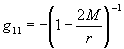 is undefined at r = 2M (remember that we are using
geometric units here).
Therefore, the Schwarzschild solution is not valid for
is undefined at r = 2M (remember that we are using
geometric units here).
Therefore, the Schwarzschild solution is not valid for
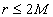 . Hence
the Schwarzschild solution is only valid for r >
max{2M,rB}.
. Hence
the Schwarzschild solution is only valid for r >
max{2M,rB}.
 In this setting of the spherical mass M, we define the value
rS = 2M as
the Schwarzschild radius of the mass. If the mass has a radius less
than rS, then it is called a black hole. In that case, the surface
r =rS is called the event horizon
of the black hole.
In this setting of the spherical mass M, we define the value
rS = 2M as
the Schwarzschild radius of the mass. If the mass has a radius less
than rS, then it is called a black hole. In that case, the surface
r =rS is called the event horizon
of the black hole.
 In "traditional" units, the Schwarzschild radius of an object of mass
M is rS = 2GM/c2.
For the Sun, rS = 2.95 km and for Earth,
rS = 8.86 mm.
So if the Earth were compressed down to about the size of a pea, then it would
be at the density of a black hole.
In "traditional" units, the Schwarzschild radius of an object of mass
M is rS = 2GM/c2.
For the Sun, rS = 2.95 km and for Earth,
rS = 8.86 mm.
So if the Earth were compressed down to about the size of a pea, then it would
be at the density of a black hole.
 We see that the Schwarzschild solution is not valid for
We see that the Schwarzschild solution is not valid for  since the
metric coefficient
since the
metric coefficient 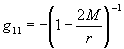 is
undefined at r = rS = 2M.
We need a new set of coordinates to explore the
behavior of the gravitational field of a black hole inside of the event
horizon.
is
undefined at r = rS = 2M.
We need a new set of coordinates to explore the
behavior of the gravitational field of a black hole inside of the event
horizon.
 Based on initial work by Arthur
Eddington in 1924 and more detailed work by David Finkelstein in 1958, a
system of coordinates was introduced which were valid for all r >
rB.
These are called the Eddington-Finklestein coordinates.
Based on initial work by Arthur
Eddington in 1924 and more detailed work by David Finkelstein in 1958, a
system of coordinates was introduced which were valid for all r >
rB.
These are called the Eddington-Finklestein coordinates.
 We introduce the variable
We introduce the variable
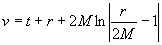 .
Then we can verify that the Schwarzschild solution becomes
.
Then we can verify that the Schwarzschild solution becomes
 This is the Schwarzschild solution in Eddington-Finkelstein
coordinates
This is the Schwarzschild solution in Eddington-Finkelstein
coordinates  .
Notice that each of the metric
coefficients is defined for all
.
Notice that each of the metric
coefficients is defined for all 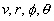 and so we can use
this version of the Schwarzschild solution to explore what happens
for all nonzero r > rB.
and so we can use
this version of the Schwarzschild solution to explore what happens
for all nonzero r > rB.
 Now let's consider what happens to photons emitted at a given distance from
the center of a black hole. We ignore
Now let's consider what happens to photons emitted at a given distance from
the center of a black hole. We ignore 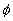 and
and 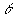 and take
and take
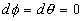 . We want to study the radial path that photons follow.
That is, we want to look at a radial lightlike geodesic. Therefore we set
. We want to study the radial path that photons follow.
That is, we want to look at a radial lightlike geodesic. Therefore we set
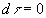 and solve. First, consider the case r >
rS. We are lead to two
equations involving t and r. The first is
and solve. First, consider the case r >
rS. We are lead to two
equations involving t and r. The first is
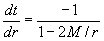 Here, dt/dr is negative for r >
rS and so as time t increases, distance
from the origin r decreases. These represent the ingoing lightlike
geodesics. The second equation in this case is
Here, dt/dr is negative for r >
rS and so as time t increases, distance
from the origin r decreases. These represent the ingoing lightlike
geodesics. The second equation in this case is
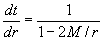 Now, dt/dr is positive
for r > rS and so as time increases, distance
from the origin r increases.
These represent the outgoing lightlike geodesics.
Therefore a flash of
light emitted at position r where r >
rS will result in photons that go
towards the black hole and photons that go away from the black hole.
Now, dt/dr is positive
for r > rS and so as time increases, distance
from the origin r increases.
These represent the outgoing lightlike geodesics.
Therefore a flash of
light emitted at position r where r >
rS will result in photons that go
towards the black hole and photons that go away from the black hole.
 Second, consider the case r < rS.
We are lead to the relationships
Second, consider the case r < rS.
We are lead to the relationships
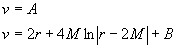 where A and B are constant.
As we will see, both of these correspond to ingoing lightlike geodesics!
Let's look at a diagram that summarizes these results.
where A and B are constant.
As we will see, both of these correspond to ingoing lightlike geodesics!
Let's look at a diagram that summarizes these results.
 Here we have a set of oblique axes r
and v. Where the curves cross, we can imagine that a photon is emitted
at these points and that the two curves represent the possible path of photons
emitted at these points.
Notice that a photon
emitted towards the center of the black hole will travel to the center of
the black hole (or at least to rB).
A photon emitted away from the
center of the black hole will escape the black hole if it is emitted at
r > rS. However, such photons are "pulled"
towards r = 0 if they are
emitted at r < rS.
Therefore, any light emitted at r < rS will not
escape the black hole and therefore cannot be seen by an observer located
at r > rS. Thus the name black hole.
Similarly, an observer
outside of the black hole cannot see any events that occur in
Here we have a set of oblique axes r
and v. Where the curves cross, we can imagine that a photon is emitted
at these points and that the two curves represent the possible path of photons
emitted at these points.
Notice that a photon
emitted towards the center of the black hole will travel to the center of
the black hole (or at least to rB).
A photon emitted away from the
center of the black hole will escape the black hole if it is emitted at
r > rS. However, such photons are "pulled"
towards r = 0 if they are
emitted at r < rS.
Therefore, any light emitted at r < rS will not
escape the black hole and therefore cannot be seen by an observer located
at r > rS. Thus the name black hole.
Similarly, an observer
outside of the black hole cannot see any events that occur in
 and so (again) the sphere r = rS
is called the event horizon of the black hole.
and so (again) the sphere r = rS
is called the event horizon of the black hole.
Notice the worldline of a particle which falls into the black
hole. If it periodically releases a flash of light, then the outside
observer will see the time between the flashes getting longer and longer.
There will therefore be a gravitational redshift of
photons emitted near r = rS with r >
rS. Also notice that the outside
observer will see the falling particle take longer and longer to reach
r = rS. Therefore the outside observer
sees this particle fall towards
r = rS, but the particle appears to move
slower and slower. On the other
hand, if the falling particle looks out at the outside observer, it sees
things happen very quickly for the outside observer. In fact, the falling
particle will see the whole evolution of the universe to
 . All
this action, though, is compressed into the brief amount of time (in the
particles frame) that it takes to fall to r =
rS.
. All
this action, though, is compressed into the brief amount of time (in the
particles frame) that it takes to fall to r =
rS.
Notice that some of the radial lightlike geodesics
have an asymptote at r = rS. This will result in
lightcones tilting over towards the black hole as we approach r =
rS.
 Again, far from the black hole,
light cones are as they appear in flat spacetime. For
Again, far from the black hole,
light cones are as they appear in flat spacetime. For
 and
r > rS, light cones tilt over towards the
black hole, but photons can
still escape the black hole. At r = rS,
photons are either trapped at
r = rS
(those emitted radially to the black hole) or are drawn into the
black hole. For r < rS,
all worldlines are directed towards r = 0.
Therefore anything inside rS will be drawn to
r = 0. All matter in
a black hole is therefore concentrated at r = 0 in a
singularity of infinite density.
and
r > rS, light cones tilt over towards the
black hole, but photons can
still escape the black hole. At r = rS,
photons are either trapped at
r = rS
(those emitted radially to the black hole) or are drawn into the
black hole. For r < rS,
all worldlines are directed towards r = 0.
Therefore anything inside rS will be drawn to
r = 0. All matter in
a black hole is therefore concentrated at r = 0 in a
singularity of infinite density.
Go to next section.
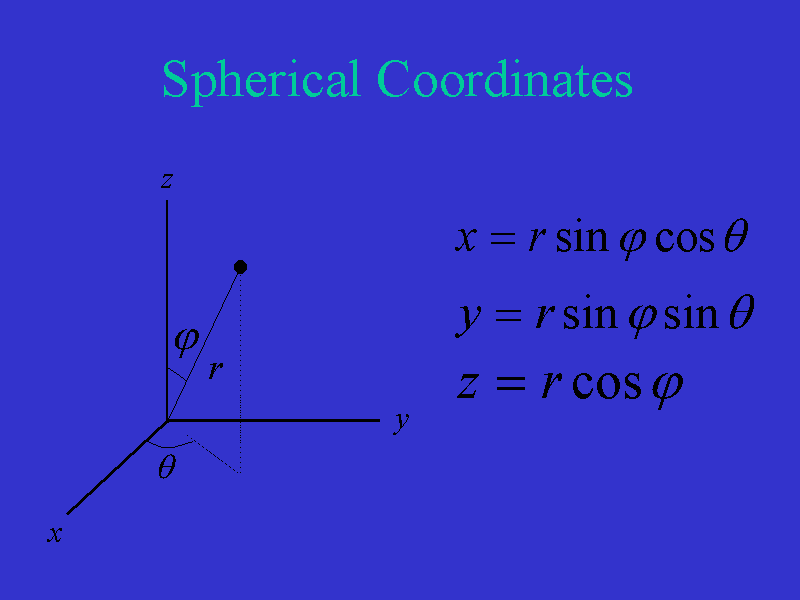
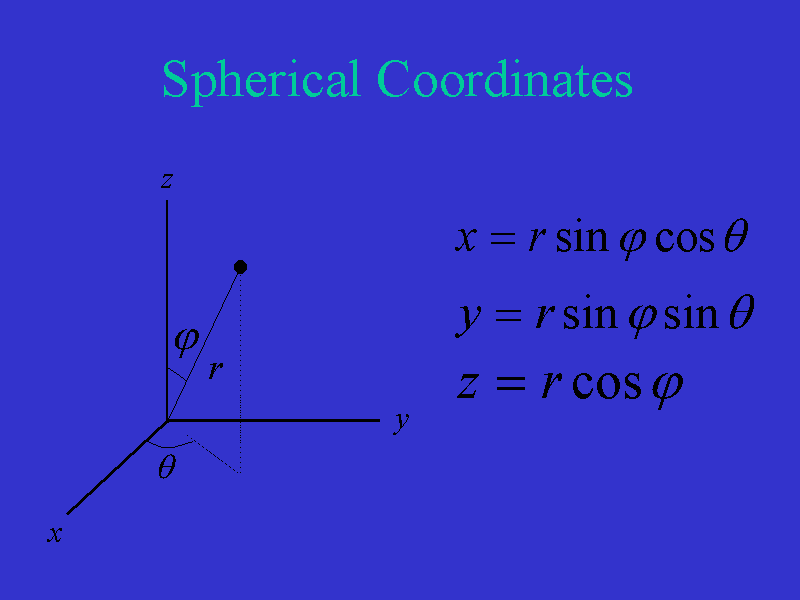
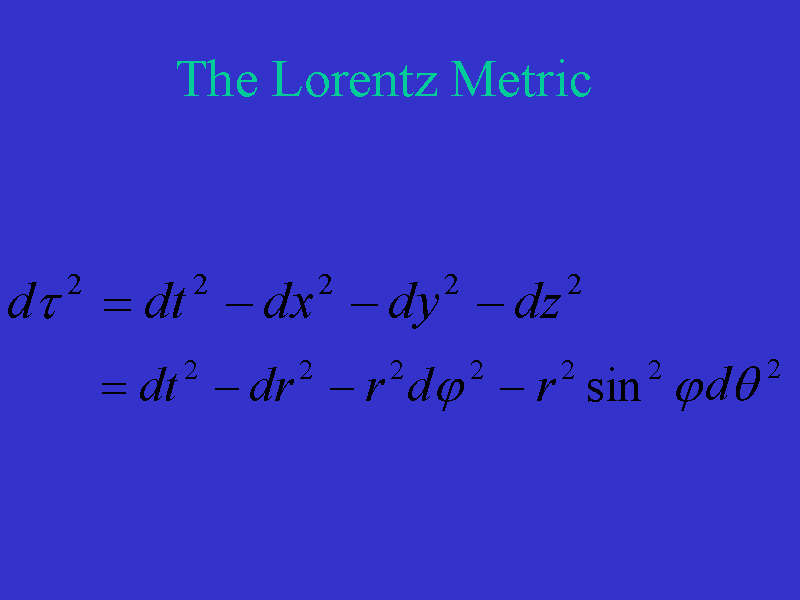


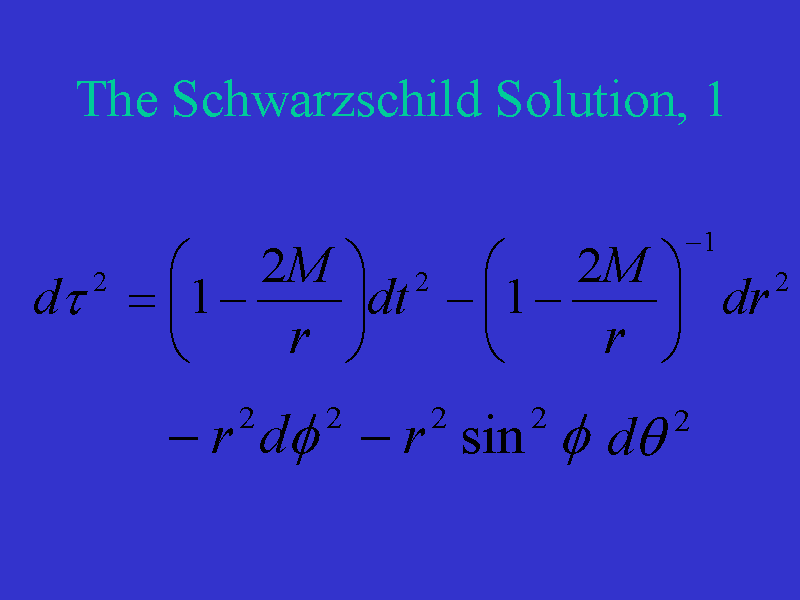










![]() . All
this action, though, is compressed into the brief amount of time (in the
particles frame) that it takes to fall to r =
rS.
. All
this action, though, is compressed into the brief amount of time (in the
particles frame) that it takes to fall to r =
rS.
