Relativity and Black Holes
Curvature and Geometry
Perhaps you have heard it said that according to relativity theory,
spacetime is "bent" or "curved" in the presence of mass. Let's
explore what this really means.
 A curve in 3-dimensional Euclidean space is a vector valued
function of a parameter t:
A curve in 3-dimensional Euclidean space is a vector valued
function of a parameter t:
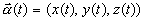 If
If 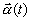 describes the location of
a particle at time t, then
describes the location of
a particle at time t, then
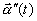 is the velocity vector and
is the velocity vector and 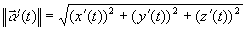 is the acceleration vector. The
speed of the particle is the scalar function defined as the magnitude
of the velocity function:
is the acceleration vector. The
speed of the particle is the scalar function defined as the magnitude
of the velocity function:
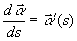
 If
If 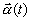 is parameterized in terms of s
such that
is parameterized in terms of s
such that 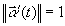 is a unit
vector tangent to curve
is a unit
vector tangent to curve  , then
, then
 is said to be
parameterized in terms of arclength. Notice that with such a
parameterization, the speed function is a constant:
is said to be
parameterized in terms of arclength. Notice that with such a
parameterization, the speed function is a constant:
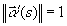 .
We can think of
.
We can think of 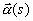 as describing a
particle that moves uniformly along the curve
as describing a
particle that moves uniformly along the curve  .
.
 In general, a particle traveling in space can accelerate in two
fundamental ways:
In general, a particle traveling in space can accelerate in two
fundamental ways:
- it can go faster or slower in its direction of travel, or
- it can change its direction of travel.
This means that if 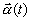 is a particle's position at time
t,
then its acceleration
is a particle's position at time
t,
then its acceleration 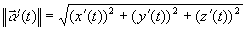 can be written as
can be written as
 a sum of a vector in the direction of travel and a vector perpendicular to
the direction of travel. The component of acceleration in the direction of
travel reflects how the particle is speeding up or slowing down. The other
component reflects how the particle is changing direction. Therefore if we
parameterize
a sum of a vector in the direction of travel and a vector perpendicular to
the direction of travel. The component of acceleration in the direction of
travel reflects how the particle is speeding up or slowing down. The other
component reflects how the particle is changing direction. Therefore if we
parameterize  in terms of arclength, then the only component
of acceleration will be the component which reflects a change in direction.
When we discuss curvature, this is what we are interested in.
in terms of arclength, then the only component
of acceleration will be the component which reflects a change in direction.
When we discuss curvature, this is what we are interested in.
 The curvature k(s) of a curve
The curvature k(s) of a curve 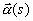 which is
parameterized in terms of arclength is the magnitude of the acceleration
vector
which is
parameterized in terms of arclength is the magnitude of the acceleration
vector 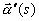 .
.
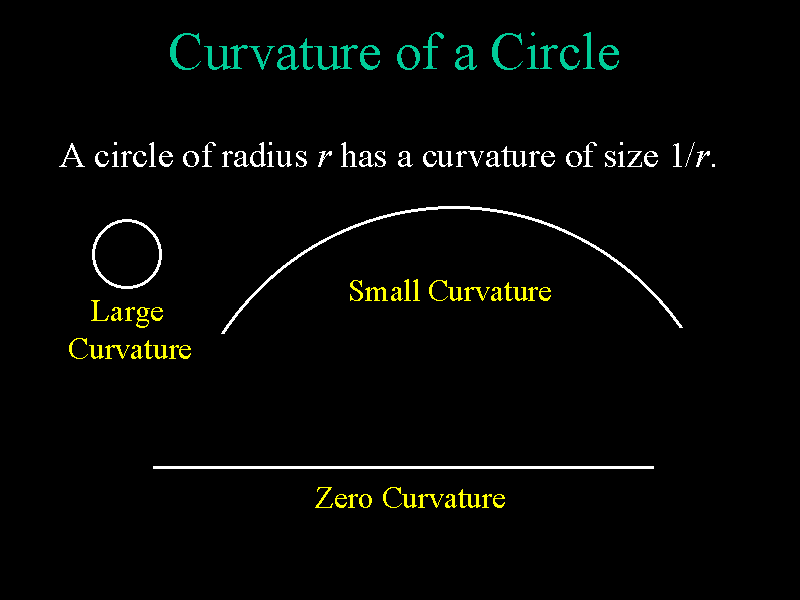 A circle of radius r has a curvature of size 1/r. Therefore, small
circles have large curvature and large circles have small curvature. The
curvature of a line is 0. In general, an object with zero curvature is
"flat."
A circle of radius r has a curvature of size 1/r. Therefore, small
circles have large curvature and large circles have small curvature. The
curvature of a line is 0. In general, an object with zero curvature is
"flat."
 Informally, we can talk about the curvature of a surface in terms of how
the surface interacts with tangent planes.
Informally, we can talk about the curvature of a surface in terms of how
the surface interacts with tangent planes.
- A surface has positive curvature at a point P if a plane
tangent to the surface at point P lies (locally) on one side of the
surface and intersects the surface (locally) only at P.
- A surface has negative curvature at a point P if a plane
tangent to the surface at point P lies (locally) on both sides of the
surface.
- A surface has zero curvature at a point P if a tangent
plane to the surface at point P lies (locally) on one side of the
surface and intersects the surface on a set that
includes a line segment containing P.
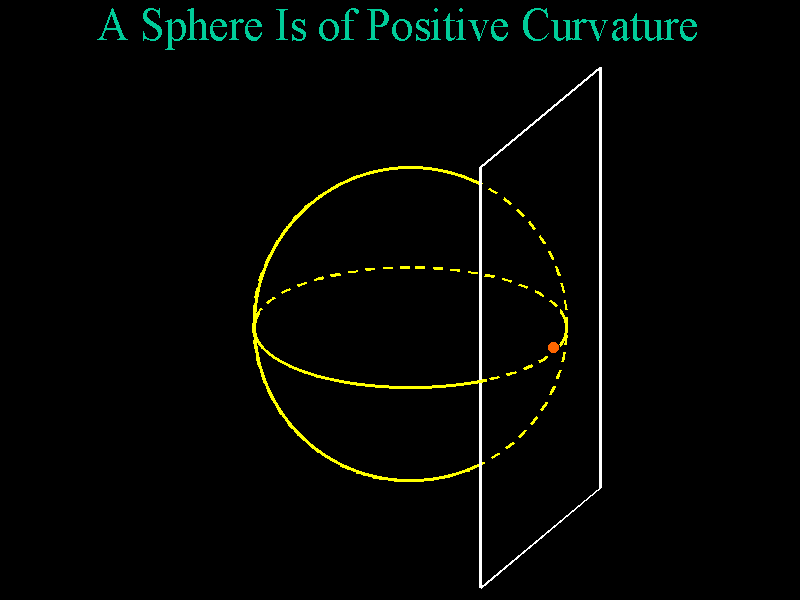 >
For example, a plane tangent to a sphere lies entirely on one side of the
sphere, and so a sphere is of positive curvature. In fact, a sphere of
radius r is of curvature 1/r2.
>
For example, a plane tangent to a sphere lies entirely on one side of the
sphere, and so a sphere is of positive curvature. In fact, a sphere of
radius r is of curvature 1/r2.
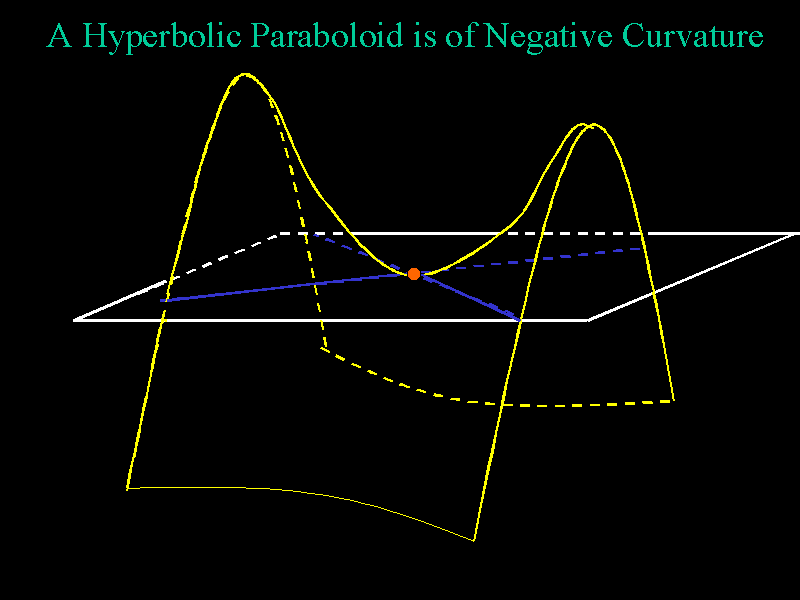 A saddle shaped
surface (or more precisely, a hyperbolic paraboloid) is of negative
curvature. A tangent plane lies on both sides of the surface. Here, the point
of tangency is red and the points of intersection are blue. Pringles potato
chips are familiar examples of sections of a hyperbolic paraboloid.
A saddle shaped
surface (or more precisely, a hyperbolic paraboloid) is of negative
curvature. A tangent plane lies on both sides of the surface. Here, the point
of tangency is red and the points of intersection are blue. Pringles potato
chips are familiar examples of sections of a hyperbolic paraboloid.
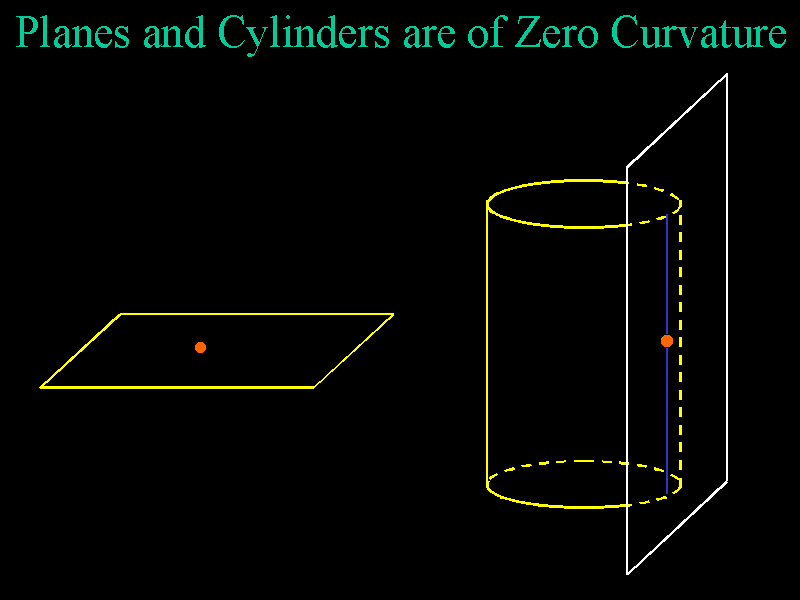 A cylinder is of zero
curvature since a tangent plane lies on one side of the cylinder and the
points of intersection (here in blue) are a line containing the point of
tangency. Also, of course, a plane is of zero curvature.
A cylinder is of zero
curvature since a tangent plane lies on one side of the cylinder and the
points of intersection (here in blue) are a line containing the point of
tangency. Also, of course, a plane is of zero curvature.
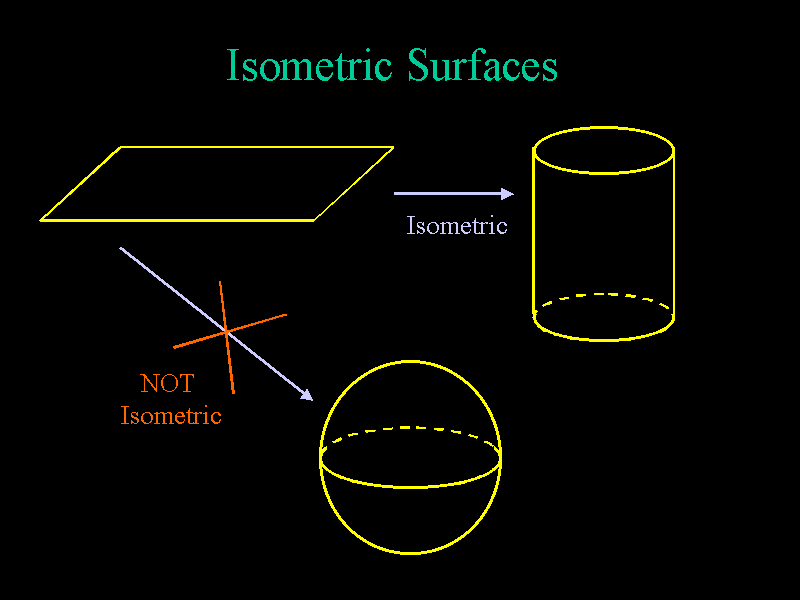 If two surfaces have the same curvature, we can smoothly transform one into
the other without changing distances (the transformation is called an
isometry). For example, a sheet of paper (used here to represent a
curvature zero plane) can be rolled up to form a cylinder (which also has
zero curvature). However, we cannot role the paper smoothly into a sphere
(which is of positive curvature).
For example, if we try to giftwrap a basketball, then the paper will overlap
itself and have to be crumpled. We also cannot role the paper smoothly
over a saddle shaped surface (which is of negative curvature) since this
would require ripping the paper.
If two surfaces have the same curvature, we can smoothly transform one into
the other without changing distances (the transformation is called an
isometry). For example, a sheet of paper (used here to represent a
curvature zero plane) can be rolled up to form a cylinder (which also has
zero curvature). However, we cannot role the paper smoothly into a sphere
(which is of positive curvature).
For example, if we try to giftwrap a basketball, then the paper will overlap
itself and have to be crumpled. We also cannot role the paper smoothly
over a saddle shaped surface (which is of negative curvature) since this
would require ripping the paper.
The curvature of a surface is also related to the geometry of the surface.
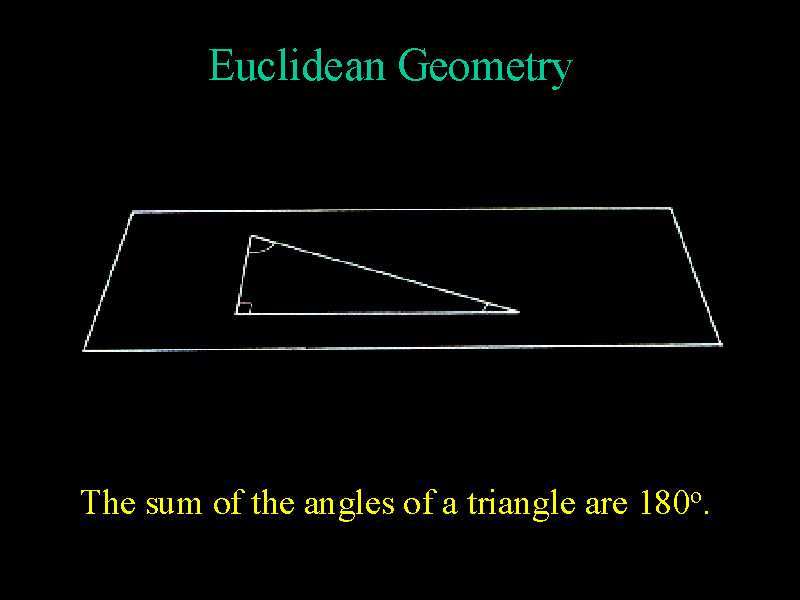 For example, on a surface of zero curvature, the geometry is the usual
Euclidean geometry in which the Parallel Postulate holds and the sum of
the angles of a triangle are 180o.
For example, on a surface of zero curvature, the geometry is the usual
Euclidean geometry in which the Parallel Postulate holds and the sum of
the angles of a triangle are 180o.
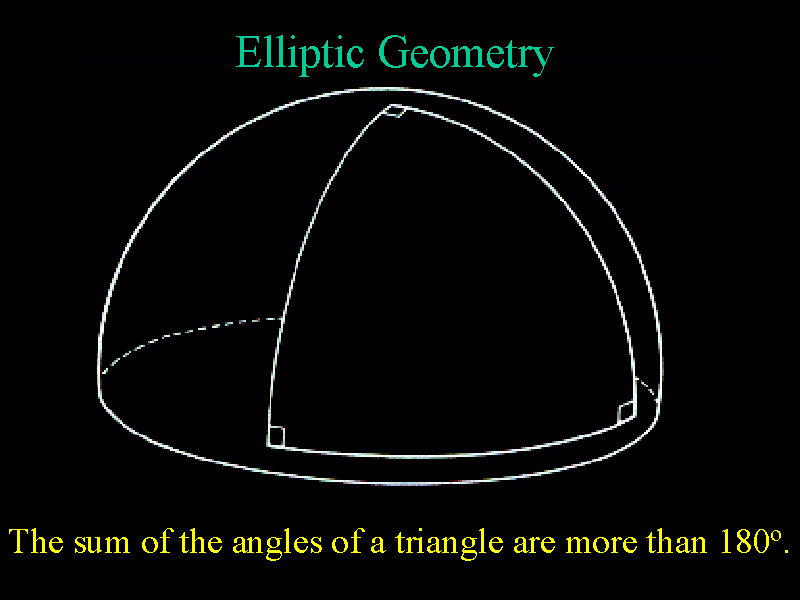 On a surface of positive
curvature, the geometry is called elliptic geometry. In this case,
the sum of the angles of a triangle is greater than 180o.
On a surface of positive
curvature, the geometry is called elliptic geometry. In this case,
the sum of the angles of a triangle is greater than 180o.
 On a
surface of negative curvature, the geometry is called hyperbolic
geometry and the sum of the angles of a triangle is less than
180o.
On a
surface of negative curvature, the geometry is called hyperbolic
geometry and the sum of the angles of a triangle is less than
180o.
 An n-manifold is, in a crude sense, an n-dimensional surface.
For
example, the spatial components of our universe form a 3-manifold and the
Minkowski spacetime in which we live is a 4-manifold. The curvature of a
manifold is not a single number, though. It is described by an object
called a tensor. For an n-dimensional manifold, the
curvature is
given by the Riemann-Christoffel curvature tensor which has
n2(n2-1)/12
independent components (when n>1). Einstein's general theory of
relativity gives the components of this tensor (and therefore the curvature
of spacetime) in the presence of mass.
An n-manifold is, in a crude sense, an n-dimensional surface.
For
example, the spatial components of our universe form a 3-manifold and the
Minkowski spacetime in which we live is a 4-manifold. The curvature of a
manifold is not a single number, though. It is described by an object
called a tensor. For an n-dimensional manifold, the
curvature is
given by the Riemann-Christoffel curvature tensor which has
n2(n2-1)/12
independent components (when n>1). Einstein's general theory of
relativity gives the components of this tensor (and therefore the curvature
of spacetime) in the presence of mass.
Go to next section.








 >
>






