Exercises

Find the velocity and acceleration of the following vector-valued functions:

1. r( t) = á t2,t3,t4 ñ 2. r( t) = át2,t5,t4 ñ 3. r( t) = át-1,t-2,t-3/2 ñ 4. r( t) = á ( t2-1) 1/2,( t2+1)-1,1 ñ 5. r( t) = á 3cos( t) ,5sin( t) ,4cos( t) ñ 6. r( t) = á 3cos( t) ,5sin( t),4cos( t) ñ 7. r( t) = á tan( t) ,cot( t) ,csc( t) ñ 8. r( t) = á et,e-t,ln( t2+1) ñ 9. r( t) = á 1,1,ln[ sec(t) ] ñ 10. r( t) = á 2,3,1 ñ et- á 1,4,7 ñ e-t 11. r( t) = t2i+tan-1( t) j 12. r( t) = i+t j+t2 k 13. r( t) = e-t á sin( t),cos( t) ,t ñ 14. r(t) = tan( t) á sin( t) ,cos( t) ,sec( t) ñ

Find the velocity at the given time and sketch it along with the curve r( t).

15. r( t) = á t2,t4 ñ,  t = 1 16. r( t) = á2t,64-16t2 ñ , t = 1 17. r( t) = á cos( t) ,sin( t) ñ ,  t = p 6 18. r( t) = á cos( t) ,sin( t) ñ ,  t = p 6 19. r( t) = á et,e-t ñ,  t = 0 20. r( t) = á tan(t) ,sec( t) ñ ,  t = p 4 21. r( t) = á 3t+1,2t+3 ñ ,  t = 2 22. r( t) = á bt2,2bt ñ,  t = 1

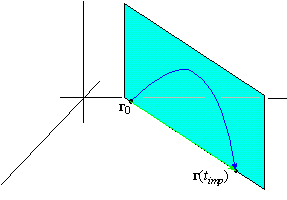
Find r( t) for the given initial conditions using antidifferentiation, and then find the plane of motion, the time to maximum height, the maximum height, the time of impact, and the point of impact of the projectile.

23. r0 = á 0,0,0 ñ 24. r0 = á 0,0,0 ñ v0 = á 1,2,64 ñ v0 = á 1,1,96 ñ 25. r0 = á 1,3,0 ñ 26. r0 = á 2,1,3 ñ v0 = á 72,38,65 ñ v0 = á 1,1,0 ñ 27. r0 = á 0,0,0 ñ 28. r0 = á 0,0,0 ñ v0 = á 0,0,0 ñ r0 = á 0,0,0 ñ 29. r0 = á 0,0,0 ñ 30. r0 = á 0,0,0 ñ v0 = á 72,38,65 ñ v0 = á 72,38,65 ñ

31. In example 6 a projectile is moving near the surface of Mars, and we found that its position at time t is given by

r( t) = á 10t,20t,64t-6.1t2 ñ

Find the plane of motion, the time to maximum height, the maximum height, the time of impact, and the point of impact of the projectile, and then compare the result to example 7, in which a projectile with the same initial conditions is traveling near the earth.

32. When r₀ is in the xy-plane, then the range of the projectile-i.e., the distance the projectile travels between leaving the earth and striking the earth-is the length of the vector r( t_imp) -r₀. That is,

range = || r( timp) -r0||

Find the range of the projectile in example 7, and then find the range of the projectile in problem 31. How much farther would the projectile travel on Mars than it would on the earth? .

33. Suppose a baseball is thrown parallel to the x-axis with an initial speed of 75 m.p.h. (75 m.p.h. = 110 feet per second), and suppose that the baseball is released from the point (0,0,6  feet) .

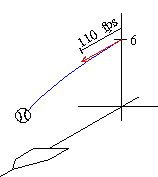
What is the position r( t) of the ball at time t? What will its position be when it crosses the plate if the distance from the mound to the plate is 60 feet, 6 inches? How long will it take for the baseball to reach the plate?

34. Repeat Exercise 33 if the baseball has an initial speed of 90 m.p.h. (90 m.p.h. = 132 feet per second).

35. Magnus Force: The spin of a baseball creates a force called the Magnus force which is perpendicular both to the direction of motion and to the axis about which the ball spins. For illustration, the axis of spin in the figure below is vertical.

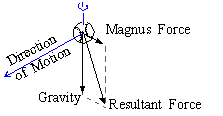
Indeed, an angular velocity of about 1500 revolutions per minute induces a Magnus force which is about 1/3 the force of gravity, so that the resultant acceleration on the ball is initially a( t) = á 0,11,32 ñ . What is the position of a ball that has this type of acceleration it its initial position and velocity are the same as in problem 33? What is the equation of its plane of motion?

36. Magnus Force: In reality, the magnus force in problem 35 is not a constant force but is given by

FM = Bm( w×v)

where B = 4.1×10^-4 for an average baseball at about 1500 rpm, m is the mass of the ball, w is the angular velocity vector, and v is the ball's velocity.

1. Explain why the acceleration of the ball is given by

   a( t) = B( w×v) -g

   where g is the acceleration due to gravity.
2. * Computer Algebra Project: If the axis of the spin is vertical, then w = k. Thus, Newton's laws of motion imply that
   

   dv dt = B( k×v) -g

   Use a computer algebra system to plot the solution to this law of motion for the initial conditions given in problem 33, and compare the result to the result in problem 35.

37. When r₀ = á 0,0,0 ñ , then the motion begins at the origin. Show that when r₀ = á 0,0,0 ñ , then t_imp = 2t_max.

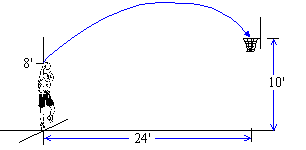
38. * A Basketball's Initial Velocity: An NBA player shoots a 3-pointer from 24 feet ( 3 point line is at 23'9''), and 1.4 seconds elapse before it passes through the hoop. If we assume that the player released the ball from a height of 8 feet, then what is the initial velocity of the ball? And what is the ball's maximum altitude?

39. Bezier Curves: The Bezier curve determined by the 4 points P₀( x₀,y₀) , P₁(x₁,y₁) , P₂( x₂,y₂) , and P₃(x₃,y₃) is the curve with endpoints P₀ and P₃ which is tangent to the vectors P₀P₁ and P₂P₃ at the points P₀ and P₃, respectively.

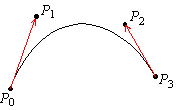
In this exercise, we show that a Bezier curve is the graph of the vector valued function

1. Compute r( 0) and r( 1) .
2. Compute v( t) , and then compute v( 0) and v( 1) .
3. Explain how (a) and (b) relate to the figure shown above.

40. Bezier Curves: Construct the Bezier curve using the parameterization in exercise 29 using the 4 points P₀( 0,0) , P₁( 0,1) , P₂( 1,1) , and P₃(1,0) , and then sketch the result along with the vectors P₀P₁ and P₂P₃.