Part 1: 3 Dimensional Vector-Valued Functions

Most of the concepts for oriented curves in 2 dimensions carries over to higher dimensions. Indeed, in R³, vector-valued functions are of the form

EXAMPLE 1    Sketch the curve parametrized by r(t) = á cos( t) ,sin( t),t ñ for t in [ 0,4p] .       

Solution: The computer algebra system Maple yields the following curve

However, it does little good to eliminate t when working with curves in R³. Instead, we must develop the calculus of vector-valued functions in R³ as a means of studying these functions directly.

To begin with, we define the limit of a vector-valued function r( t) =   á f( t) ,g( t) ,h(t) ñ to be

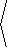
lim t® p  r( t) =  lim t® p  f( t) , lim t® p  g( t), lim t® p  h( t)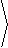

(1)

when each of these limits exist. As a result, we define the derivative of r( t) =   á f( t) ,g( t),h( t) ñ to be

dr dt = lim Dt® 0  r(t+Dt) -r( t) Dt

which via the definition of the limit (1) yields

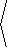dr dt =  lim Dt® 0   f( t+Dt) -f( t) Dt , lim Dt® 0  g(t+Dt) -g( t) Dt , lim Dt® 0  h( t+Dt) -h(t) Dt

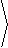Moreover, we often denote dr/dt by v and call it the velocity of r( t) . Likewise, the derivative of v( t) is often called the acceleration of r( t) . The computation above shows us that we have the following:   

Theorem 6.1: The velocity v( t) of the function r( t) =   á f( t),g( t) ,h( t) ñ  is

v( t) =  dr dt = á f ¢( t) ,g¢( t) ,h¢( t) ñ

Likewise, the acceleration of r( t) is given by

a( t) =  dv dt   = á f ¢¢( t) ,g¢¢( t) ,h¢¢( t) ñ

       

In addition, we define antiderivatives of r(t) =   á f( t) ,g( t) ,h(t) ñ to be

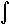r( t) dt = 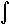f( t) dt, 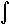g( t) dt, 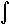h( t) dt + áC1,C2,C3 ñ

where C₁,C₂,C₃ are arbitrary constants.

       

EXAMPLE 2    Compute the velocity and acceleration of

r( t) = á t2,e2t,t3 ñ

Solution: To begin with, the velocity of r(t) is

v( t) =  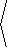d dt t2,  d dt e2t,  d dt t3  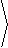 = á 2t,2e2t,3t2 ñ

As a result, the acceleration of r(t) is

a( t) =  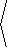d dt 2t,  d dt 2e2t,  d dt 3t2  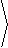  = á2,4e2t,6t  ñ