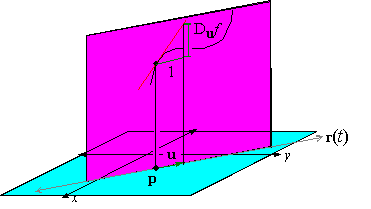
The Directional Derivative   

Let p = ( x₀,y₀) be fixed and let u = á m,n ñ be a unit vector. Then a vertical slice of z = f( x,y) is the curve formed by the intersection of the vertical plane through the line r(t) = p+ut and the surface z = f( x,y) . In particular, z( t) is the height of the surface z = f(x,y) at the point r( t) .

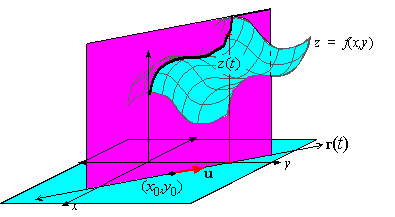
Since u is a unit vector, the point r( h) is a distance h from r( 0) . Thus, a run of h causes a rise of z( h) -z( 0)

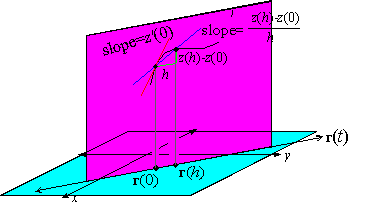
It follows that the slope of the tangent line at r( 0) is

Definition 6.1    The directional derivative of f(x,y) in the direction of a unit vector u is denoted by D_uf and is defined to be

Duf = Ñf·u

In particular, D_uf is the slope of the tangent line to the curve formed by the intersection of z = f( x,y) and the vertical plane through a point p parallel to a unit vector u.

       

For example, the ordinary partial derivatives are special cases of D_uf:

¶f ¶x = Dif        and        ¶f ¶y = Djf

That is, f_x yields slopes of vertical slices in the xz-plane and f_y yields slopes of vertical slices in the xy-plane.       

EXAMPLE 3    Find the derivative of f( x,y) = 1.1x² - 0.1xy in the direction of v = á 3,4 ñ.       

Solution: Since v is not a unit vector, we first finds its direction vector:

u =  1 v v =  1 5 á 3,4 ñ =  3 5 ,  4 5   = á 0.6, 0.8 ñ

The gradient of f is Ñf = á 2.2x - 0.1y, -0.1x ñ, so that

Du  f   =   á 2.2x - 0.1y, -0.1x ñ · á 0.6, 0.8 ñ =   0.6( 2.2x - 0.1y) + 0.8 (-0.1x ) =   1.24x - 0.06y

LiveGraphics3d Applet