DIFF GEOM: Geodesics

The material in this chapter brings us very close to an extremely important field of mathematics known as Differential Geometry.  The "DIFF GEOM" material at the end of this chapter and in a few places in chapter 5 comprises an introduction to this extremely important field.  The "DIFF GEOM" material may be omitted completely without compromising the course, but we felt that such proximity to this important body of mathematics justified including this material for those inclined to pursue it.

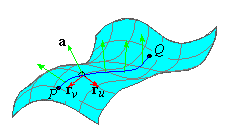
Let's begin with the concept of a geodesic.  Suppose that r( u,v) is the parameterization of a surface and that r( t) = r( u(t) ,v( t) ) is a curve on that surface.  If the acceleration r'' (t) is normal  to the surface at each point on the curve, then r( t) is said to be a geodesic on r( u,v). Equivalently, r( t) = r( u(t) ,v( t) ) is a geodesic only if r'' · r_u = 0 and r'' · r_v = 0. That is, a geodesic does not curve in any tangent plane to the surface, which means that geodesics are the ''straightest'' curves on a surface. The concept of a geodesic is illustrated by the animation below: Clicking on the animation will switch to a different view.

EXAMPLE 1    Let r( u,v) = á cos( u) ,sin( u) ,v ñ be a parameterization of the right circular cylinder, and let r( t) = r( t,2t+1) be a curve on that surface. Show that r( t) is a geodesic on the cylinder.      

Solution: The expression r( t,2t+1) implies that u = t and v = 2t+1. Thus, r( t) = ácos( t) ,sin( t) ,2t+1 ñ , so that

r' ( t) = á -sin( t),cos( t) ,2 ñ         and        r''( t) = á -cos( t),-sin( t) ,0 ñ

Since r_u = á -sin( u) ,cos(u) ,0 ñ and r_v = á0,0,1 ñ and since u = t, we have

r'' · ru = cos( t)sin( u) -cos( u) sin( t) = cos( t) sin( t) -cos( t) sin( t) = 0

Likewise, r'' ·  r_v = 0·cos( t) -0·sin( t) +2·0 = 0. Thus, r( t) = r( t, 2t+1) is a geodesic on the cylinder.

LiveGraphics3d Applet

In general, the geodesics on the plane are straight lines, and the geodesics on the right circular cylinder parameterized by

r( u,v) = á cos( u) ,sin(u) ,v ñ

are the images of the straight lines after the plane has been rolled up into a cylinder-i.e., circles, vertical lines, and helices that are curves of the form

g( t) = r( at+b,ct+d)

where a, b, c, and d are constants.

In fact, if a surface r( u,v) contains a straight line L( t) = mt+b, then L^¢( t) = m and L^¢¢( t) = 0. Thus, L^¢¢· r_u = 0 and L^¢¢· r_v = 0, which implies that any straight line contained within a surface must be a geodesic of the surface.        

EXAMPLE 2    Show that the catenoid x²+y²-z² = 1 can be parameterized by

r( u,v) = á cos(v)-usin( v),sin( v) +ucos( v) ,u ñ ,  u in ( -¥,¥) ,  v in [ 0,2p]

and then show that g( t) = r(t,q) is a straight line for each fixed value of q in [ 0,2p] . Solution: Since x = cos( v) -usin( v) and y = sin( v) +ucos( v) , we have

x2+y2 = ( cos( v) -usin( v) )2+( sin( v) +ucos( v) ) 2 = cos2( v) -2ucos( v) sin( v)+u2sin2( v) +sin2( v) +2ucos( v) sin( v)+u2cos2( v) = cos2( v) +sin2( v) +u2( cos2( v) +sin2( v) ) = 1+u2

Thus, x²+y²-z² = 1 since z = u. The curve

g( t) = á cos(q)-tsin(q) ,sin( q) +tcos( q),t ñ

has a derivative of g^¢( t) = á -sin( q) ,cos( q),1 ñ , so that g^¢¢(t) = 0 (differentiation is in the variable t) and g( t) must be a straight line. The lines are geodesics of the catenoid and are shown in the figure below:

LiveGraphics3d Applet

In addition, if r'' is normal to the surface, then the tangential acceleration of r( t) is zero and consequently, a geodesic r( t) has constant speed. For example, the speed of the geodesic in example 3 is Ö5 and the speed of the great circle in example 4 is 1. Since the speed of a geodesic is constant, the arclength is proportional to the parameter, and as a result, it is rather simple to obtain an arclength parameterization of a geodesic.