Line Integrals as Pull-Backs

If M  and N  are infinitely-differentiable functions of x  and y , then an expression of the form Mdx+Ndy is known as a differential form . Typically, a differential form is defined along a curve C:   r ( t ) = ,  t in [ a,b ], in terms of the parameter t .  That is,

Mdx+Ndy = M     +   N    

In 3-dimensional space, differential forms are given by Mdx+Ndy+Pdz where M, N, and P  are infinitely differentiable in x, y, and z ;   and likewise, a differential form  is defined along a curve C: r ( t ) = ,   t in [ a,b ], by

Mdx + Ndy + Pdz = M     +   N    + P

In both cases, we say that the differential form is pulled back  to the parameter t.  

We can use the idea of a pullback to define the line integral of a differential form Mdx+Ndy+Pdz along a curve C: r ( t ) = ,   t in [ a,b ], by

 =

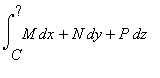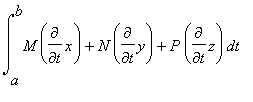
Let's look at an example:  Let's evaluate

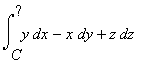
over the curve C: r ( t ) = ,    t in .    First, let's define the differential form and the curve.

>	SetCoordinates( cartesian[x,y,z] ); diff_form:=y*dx-x*dy+z*dz; r:=<cos(t),sin(t),t>;

>

To obtain the pullback, we replace dx, dy, and  dz by the derivatives of x, y, and z , respectively, along the curve.

>	diff_form:=subs(dx=Diff(r[1],t),dy=Diff(r[2],t),dz=Diff(r[3],t),diff_form); diff_form:=value(%);

>

Finally, we construct the integral of the pullback into the t  variable, substitute for x, y, and z , and evaluate.

>	Int(diff_form,t=0..2*Pi); subs(x=r[1],y=r[2],z=r[3],%); value(%);

>

If we let F ( x,y,z ) =   and let d r = , then the line integral of a differential form can be written

picture--F.dr

Indeed, this is the form that Maple prefers to work with.  The command Lineint  in the "VectorCalculus" package will calculate a line integral of a vector field F  over an oriented curve C, which it refers to as a "Path".  

For example, lets evaluate

over the curve C: r ( t ) = ,    t in  by applying the Lineint  command to the vectorfield

F ( x,y,z ) =  

along the Path C :        ,    .  The option "inert" allows us to see the pullback integral before it is evaluated.

>	LineInt( VectorField( <y,-x,z> ), Path( <cos(t),sin(t),t>, t=0..2*Pi ),'inert' ); value(%);

>

The result should be the same as before