Wires and Solenoids
A solenoidal vector field is a vector field B that satisfies
div( B ) = 0
Solenoidal fields occur frequently in the study of electricity and magnetism as magnetic fields produced by wires and solenoids (a solenoid is a tightly wound coil of wire).
It can be shown (see exercise 7) that if B is solenoidal, then there is a vector field A for which
B = curl( A )
The vector field
A
is often called the
vector potential
for the (usually magnetic field)
B
. Moreover, if surfaces
![]() and
and
![]() share a common boundary curve
share a common boundary curve
![]() and if
B
is solenoidal with vector potential
A
, then
and if
B
is solenoidal with vector potential
A
, then
![[Maple OLE 2.0 Object]](images/5-612.gif)
However, since
B
= curl(
A
), this says that if surfaces
![]() and
and
![]() share a common boundary curve, then
share a common boundary curve, then
![[Maple OLE 2.0 Object]](images/5-615.gif)
That is, the Flux of a solenoidal field is independent of the surface through which it is measured.
Let's look at an example. Let's suppose that the y axis represents an infinitely long wire with a circular cross-section, and let's suppose a current of I amps is passed through the wire. Then the current vector is given by I = I j and the moving charges induce a magnetic field of the form
B =
![1/2/Pi/epsilon[0]/(c^2)](images/5-616.gif)
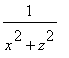 I
x
I
x
![]()
where
![]() is the dielectric constant and
c
is the speed of light. Let's show that
B
is solenoidal and then examine its graph when .
is the dielectric constant and
c
is the speed of light. Let's show that
B
is solenoidal and then examine its graph when .
| > | SetCoordinates(cartesian[x,y,z]): B:=VectorField(I/(2*Pi*epsilon[0]*c^2*(x^2+z^2))*(<0,1,0>&x<x,0,z>)); Div_B:=Divergence(B); |
| > |
Now let's examine the graph of the vector field when
![I/(epsilon[0]*c^2) = 1](images/5-620.gif) along with the "wire" in blue.
along with the "wire" in blue.
| > | fieldplot3d(subs(I=epsilon[0]*c^2,B),x=-1..1,y=-1..1,z=-1..1,color=red,grid=[12,7,12]): display(%,spacecurve([0,t,0],t=-1.2..1.2,color=blue,thickness=5)); |
| > |
Clearly, the flow of the magnetic field B is the set of all circles centered on the y -axis that are parallel to the xz -plane.
Now let's suppose that we have two surfaces,
![]() which is the paraboloid
r
(
u,v
) =
which is the paraboloid
r
(
u,v
) =
 ,
r
in [0,1],
,
r
in [0,1],
![]() in
in
![]() and
and
![]() which is the upper unit hemisphere
which is the upper unit hemisphere
![]() =
=
![]() ,
,
![]() in
in
![[0, Pi/2]](images/5-629.gif) ,
,
![]() in
in
![]() .
.
| > | S1:=<r*cos(theta),r*sin(theta),1-r^2>,r=0..1,theta=0..2*Pi: S2:=<sin(phi)*cos(theta),sin(phi)*sin(theta),cos(phi)>,phi=0..Pi/2,theta=0..2*Pi: p1:=fieldplot3d(subs(I=epsilon[0]*c^2,B),x=-1..1,y=-1..1,z=-1..1,color=red,arrows=THICK): p2:=plot3d(S1,color=blue): p3:=plot3d(S2,style=wireframe,color=green): p4:=plot3d([r*cos(theta),r*sin(theta),1-r^2],r=0..1,theta=0..2*Pi,color=blue,style=wireframe): p5:=plot3d([sin(phi)*cos(theta),sin(phi)*sin(theta),cos(phi)],phi=0..Pi/2,theta=0..2*Pi,color=green): q0:=display(p1,p2,p5): q1:=display(p1,p2,p3): display(q0,q1,insequence=true,axes=normal); #Choose animate to see both surfaces |
| > |
The two surfaces share a common boundary of the unit circle. Now let's examine the Flux of B through the first surface.
| > | Flux_S1:=Flux(B,Surface(S1),'inert'); Flux_S1:=value(%); |
| > |
Now let's examine the Flux of B through the second surface:
| > | Flux_S2:=Flux(B,Surface(S2),'inert'); Flux_S2:=value(%); |
| > |
Although the first was much harder for Maple than the second, still the total flux.
The magnetic field of an ideal solenoid is constant with its "flow" parallel to the axis of the coil. Thus, it is trivally solenoidal, and repeating this section with a constant B reveals the same result.