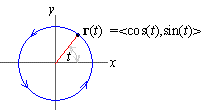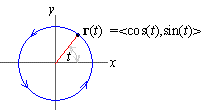Part 2: Using Identities to Eliminate the Parameter

In many instances, trigonometric identities are used to find the equation in x and y corresponding to the graph of a given vector-valued function. In particular, the following identities occur frequently in this context:

cos2( t) +sin2( t) = 1 1+tan2( t) = sec2( t) 1-2sin2(t) = cos( 2t) cosh2( t) -sinh2( t) = 1 1+cot2( t) = csc2( t) 2cos2(t) -1 = cos( 2t)

In addition, we may also on occasion use identities such as 2sin(t) cos( t) = sin( 2t) and e^te^-t = 1.      

EXAMPLE 2    Sketch the curve parameterized by r(t) = á cos( t) ,sin( t) ñ for t in [ 0,2p] .       

Solution: Since x = cos( t) and y = sin(t) , we begin with

cos2( t) +sin2( t) = 1

Substituting x = cos( t) and y = sin( t) into the identity yields

x2+y2 = 1

which is the unit circle. Moreover, the initial and terminal points are

initial: ( t = 0) x = cos( 0) = 1, y = sin( 0) = 0 terminal: ( t = 2p) x = cos( 2p) = 1, y = sin( 2p) = 0

Since the initial and terminal points are both ( 1,0) , we must determine the orientation by choosing a value of t near an endpoint of [0,2p] :

t = p 6 :    x = cos æ è p 6 ö ø = 3 2 ,    y = sin æ è p 6 ö ø = 1 2

Thus, the orientation of the curve is counterclockwise:

   

The function r( t) =   á f(t) ,g( t) ñ , t in [ a,b] , parameterizes a closed curve if r(a) = r(b) , if  f(t) and g(t) are continuous, and if the curve has a well-defined orientation. The circle in example 2 is an example of a closed curve.       

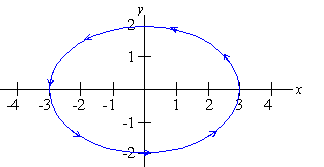
EXAMPLE 3    Sketch the curve parameterized by r(t) = á 3cos( t) ,2sin( t) ñ for t in [ 0,2p] .       

Solution: Since x = 3cos( t) and y = 2sin(t) , we begin with

cos2( t) +sin2( t) = 1

Substituting cos( t) = x/3 and sin( t) = y/2 thus yields

æ è x 3 ö ø 2   + æ è y 2 ö ø 2   = 1

If t = 0 or t = 2p, then x = 3 and y = 0. Thus, the initial and terminal points are the same and correspondingly the graph of r(t) = á 3cos( t) ,2sin( t) ñ for t in [ 0,2p] is the entire ellipse with counterclockwise orientation.

x2 9 + y2 4 = 1

       

Unfortunately, a parameterization may not define an orientation for a curve, in that the parameterization may trace the curve from the initial point to a point on the curve and then may retrace the curve back to where it started, as we will see in the next example.       

EXAMPLE 4    Find the Cartesian equation and sketch the curve r( t) = á cos( 2t) ,cos(t) ñ for t in [ 0,2p] .       

Solution: Since x = cos( 2t) and y = cos(t) , we use a double angle identity:

cos( 2t)  =  2cos2( t) -1 x  =  2y2-1

Moreover, r( 0) = á cos( 0), cos( 0) ñ = á 1,1 ñ , r( p/2) = á cos( p) ,cos( p/2) ñ = á -1,0 ñ , and r(p) = á cos( 2p) , cos( p) ñ = á1,-1ñ. Also, r( 3p/2) = ácos(3p),cos(3p/2)ñ = á -1,0 ñ and r(2p) = á cos( 4p) , cos(2 p) ñ = á1,1ñ.  Thus, the curve starts at ( 1,1) , progresses to ( -1,1) , and then retraces the curve in returning to ( 1,1) . Consequently, the orientation is not well-defined.        

EXAMPLE 5    Find the Cartesian equation of the curve

r( q) = á 2sin(q) cos(q) ,2sin2( q) ñ,  q  in  [ 0,p]

Solution: Since 2sin( q) cos( q) = sin( 2q) and 2sin²( q) = 1-cos( 2q) , we can rewrite r as

r( q) = á sin( 2q),1-cos( 2q) ñ

which implies that x = sin( 2q) and y = 1-cos(2q) . Since

sin2( 2q) +cos2( 2q) = 1

and since cos( 2q) = 1-y, we must have

x2+( y-1)2 = 1

Thus, r( q) = á 2sin( q) cos( q), 2sin²( q) ñ is a circle with radius 1 centered at ( 0,1) .