CSCI 4717: Set Associative Cache

I could've spent less time on Monday night lecturing on the overall interface of memory to the processor and more time on the organization of the cache RAM. But that isn't the way it happened, and we still have a homework assignment due this coming Monday (September 23, 2002). I am hoping that this page will make up for the ½ hour we spent discussing the set associative cache organization.

As you will recall, we discussed three cache mapping functions, i.e., methods of addressing to locate data within a cache.

• Direct
• Full Associative
• Set Associative

Each of these depends on two facts:

• RAM is divided into blocks of memory locations. In other words, memory locations are grouped into blocks of 2ⁿ locations where n represents an integer. The image below has n=2 indicating that for each block of memory, there are 2² = 4 memory locations.
  
  
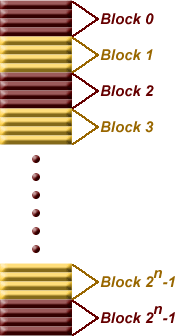
  Therefore, the least two significant bits of an address indicate the location within a block while the remaining bits indicate the block number. The table below shows an example with a 20 bit address with four words per block. Notice that for each group of four words, the word bits take on each of the four possible values allowed with 2 bits while the block identification bits remain constant.,

• The cache is organized into lines, each of which contains enough space to store exactly one block of data and a tag uniquely identifying where that block came from in memory.

As far as the mapping functions are concerned, the book did an okay job describing the details and differences of each. I, however, would like to describe them with an emphasis on how we would model them in our simulator.

Direct Mapping

Remember that direct mapping assigned each memory block to a specific line in the cache. If a line is all ready taken up by a memory block when a new block needs to be loaded, the old block is trashed. The figure below shows how multiple blocks are mapped to the same line in the cache. This line is the only line that each of these blocks can be sent to. In the case of this figure, there are 8 bits in the block identification portion of the memory address.

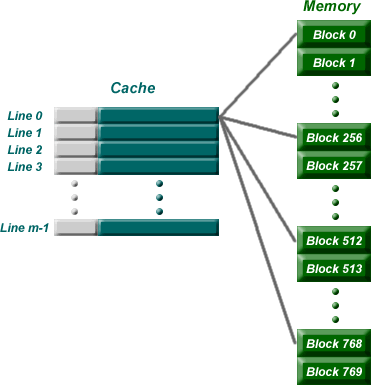
The address is broken down something like the following:

Once the block is stored in the line of the cache, the tag is copied to the tag location of the line.

Direct Mapping Summary

The address is broken into three parts: (s-r) MSB bits represent the tag to be stored in a line of the cache corresponding to the block stored in the line, r bits in the middle identifying which line the block is always stored in, and the w LSB bits identifying each word within the block. This means that:

• The number of addressable units = 2^s+w words or bytes
• The block size (cache line width not including tag) = 2^w words or bytes
• The number of blocks in main memory = 2^s (i.e., all the bits that are not in w)
• The number of lines in cache = m = 2^r
• The size of the tag stored in each line of the cache = (s - r) bits

Direct mapping is simple and inexpensive to implement, but if a program accesses 2 blocks that map to the same line repeatedly, the cache begins to thrash back and forth reloading the line over and over again meaning misses are very high.

Full Associative Mapping

In full associative, any block can go into any line of the cache. This means that the word id bits are used to identify which word in the block is needed, but the tag becomes all of the remaining bits.

Full Associative Mapping Summary

The address is broken into two parts: a tag used to identify which block is stored in which line of the cache (s bits) and a fixed number of LSB bits identifying the word within the block (w bits). This means that:

• The number of addressable units = 2^s+w words or bytes
• The block size (cache line width not including tag) = 2^w words or bytes
  
• The number of blocks in main memory = 2^s (i.e., all the bits that are not in w)
  
• The number of lines in cache is not dependent on any part of the memory address
• The size of the tag stored in each line of the cache = s bits
  

Set Associative Mapping

This is the one that you really need to pay attention to because this is the one for the homework. Set associative addresses the problem of possible thrashing in the direct mapping method. It does this by saying that instead of having exactly one line that a block can map to in the cache, we will group a few lines together creating a set. Then a block in memory can map to any one of the lines of a specific set. There is still only one set that the block can map to.

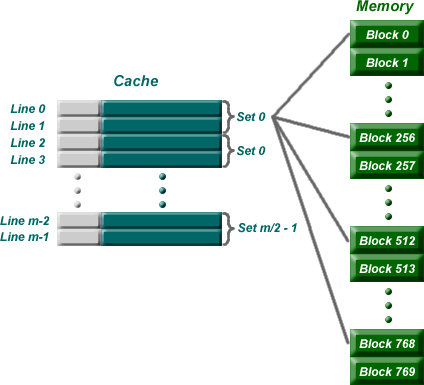
Note that blocks 0, 256, 512, 768, etc. can only be mapped to one set. Within the set, however, they can be mapped associatively to one of two lines.

The memory address is broken down in a similar way to direct mapping except that there is a slightly different number of bits for the tag (s-r) and the set identification (r). It should look something like the following:

Now if you have a 24 bit address in direct mapping with a block size of 4 words (2 bit id) and 1K lines in a cache (10 bit id), the partitioning of the address for the cache would look like this.

If we took the exact same system, but converted it to 2-way set associative mapping (2-way meaning we have 2 lines per set), we'd get the following:

Notice that by making the number of sets equal to half the number of lines (i.e., 2 lines per set), one less bit is needed to identify the set within the cache. This bit is moved to the tag so that the tag can be used to identify the block within the set.

Homework Assignment

So what do we have to do for the assignment. First of all, I've given you a class declaration again. (Sorry Java guys, the declaration is in C++. You'll just have to convert.)

class SetAssociativeCache
{
public:
    void SetAssociativeCache(
        unsigned int tag_bits,
        unsigned int set_bits,
        unsigned int word_bits,
        unsigned int lines_per_set);

    bool requestMemoryAddress(unsigned int address);

    unsigned int getPercentageOfHits(void);
}

Okay, so you have a constructor that requests the number of bits used by the tag (s-r), the number of bits used by the set identifier (r), and the number of bits used to identify the word within a block (w). Lastly, you need to define the number of cache lines per set. If the cache is a 2-way set associative, then this value will be 2. Note that for a k-way set associative cache, k must be a power of two.

There are two functions for this class too: requestMemoryAddress and getPercentageOfHits. The first one, requestMemoryAddress, is called to simulate a request to the cache. The integer is an address. Note that this isn't a pointer! It is an integer that is supposed to represent the address of the desired data. Assume that the cache is empty to start with, so your very first call to this function will require a figurative "loading of the cache".

As far as our replacement algorithm goes, if all of the lines of a set are filled with valid blocks, then you should replace the least used. This is the Least Frequently Used (LFU) algorithm discussed in the textbook.

The second function, getPercentageOfHits, is called to simply see how well the cache is performing. It should return an integer from 0 to 100 representing the percentage of successful hits in the cache. The equation should be something like: