Although the set of notes you have requested is presented below, it has not been maintained since January, 2003. All of the information in these notes has been included in an on-line text titled Computer Organization and Design Fundamentals. The book is available in three formats, two of which are free electronic downloads. Please visit one of the following links in order to access the format you prefer.
Thank you for your interest in this textbook. Please feel free to e-mail me at tarnoffetsu.edu if you have any questions or comments.
-Dave Tarnoff
Learning how to convert positive integers to binary is only the first step in a long process of learning how computers represent values. In fact, we will learn next week that computers have at least three ways of representing integers in binary. All we've learned up to this point is how positive integers (including zero) are represented. Negative numbers will open up a whole new set of problems.
This set of notes, however, will focus on the problems encountered when you try to map real world values to a set of integers with an upper and a lower limit. For example, a computer that uses 8 bits to represent an integer is capable of representing 256 individual values from 0 to 255. Temperature, however, is a floating-point value with no real upper limit. How does a computer handle this?
Digital signals by themselves can only take on two values: logic 1 and logic 0. The real world, however, is analog. Where a digital value is a one or a zero, an analog value is equivalent to a floating-point number. Temperatures do not take on quantized levels such as a boolean "on" or "off" or an integer 1, 2, 3, etc. Instead, a temperature can be one of an infinite number of possibilities taken out to infinite decimal places. Looking around us we see that all measurements in the real world are analog: pressure, light intensity, volume, etc. We may force a value into boolean levels such as light or dark, but there is always a range.
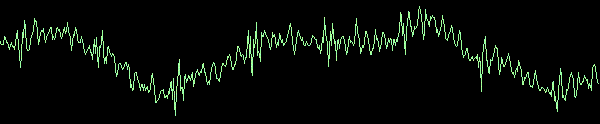
To give you an idea of the applications we are talking about, sound waves such as that from music are analog values. The image below represents such a signal.

So how does a microprocessor handle analog values when all it can communicate with is ones and zeros? An analog value created or interpreted by a computer system is not the same as an analog value in the real world. It only allows for a range defined by minimum and maximum values. The infinite number of decimal places (resolution) is gone too. Computer generated analog values are quantized to the nearest value determined by the algorithm used to convert the values. Hopefully, the resolution is small enough that the computer's accuracy is sufficient for the application.
A computer can only take a snap-shot of the current reading of an analog value. For example, a computer can only read the temperature in a room at a single moment in time. In order to record trends or detect changes, it must read the analog value over and over again at specific timed intervals. It would be like filling in the fields of a spreadsheet one at a time. In the end, you could take those measurements to create a graph to see the trends, but some information was lost in the process.
First, as was mentioned at the beginning of this section, "real world" analog values are like floating-point values with no limit on the number of digits past the decimal point. But the computer remembers an integer value. How does this work?
For a computer to read an analog value, it must define a certain range that the value must not exceed. This gives us a range on our values. For example, let's say that the computer is reading temperatures. The range of values needs to be limited to something like 0° to 120°. For a computer using 8-bit integers, this allows us to use 000000002 to represent 0° and 111111112 to represent 120°.
The number of bits used to represent an integer also defines the resolution of the analog value. In other words, the number of increments between the lowest level and the highest level is defined with the number of bits representing an integer value. For example, if a computer is using 8 bits to represent an integer, then it can record a number from 0 to 28 - 1 = 255. Therefore, our range is divided into 255 pieces.
Note that we subtract one because the binary value represents all of the measurements in the range from high to low. Since both end measurements must have a value, the number of increments is actually one less than the number of measurements.
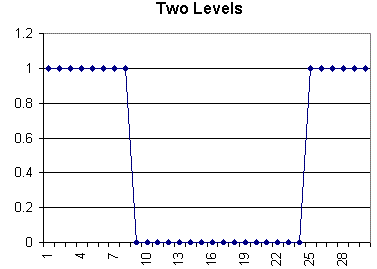
Huh? Begin by picturing a computer that represents analog values with a 1 bit integer. It can take on 21 = 2 values. The range of values is shown in the figure below.
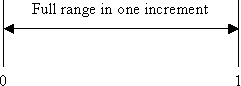
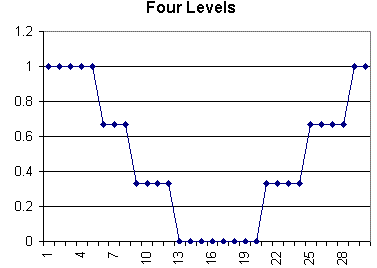
Add another bit so that we are measuring the range with 2 bits. This should give us 22 = 4 measurements or values, but notice that we only have three increments.
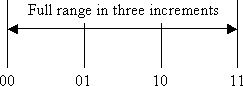
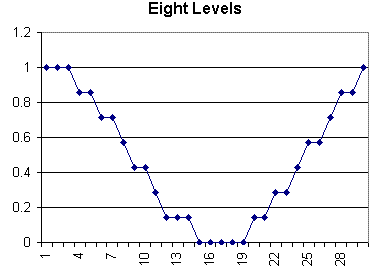
Adding yet another bit brings us to 23 = 8 measurements or values, but we only have seven increments.
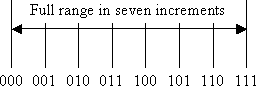
Assume that the range of our analog input to an 8-bit computer has been limited to 0 volts to 12 volts. If we assume our lowest value (0 volts) is equal to all zeros on the 8-bit output, and our highest value (12 volts) is equal to all ones on the 8-bit output, how many volts does the smallest increment of our binary output represent? E.g., if we incremented from binary 01001010 to binary 01001011, what voltage level difference does this represent?
Our voltage range is:
range = high value - low value
range = 12 volts - 0 volts
range = 12 volts
The number of increments in our range is equal to:
increments = 2n - 1 where n=number of bits
increments = 28 - 1
increments = 255
Therefore, the voltage represented by a single increment is:
Voltage increment = (voltage range)/(number of increments)
Voltage increment = 12 volts/255
Voltage increment = 0.04706 volts/increment
If we examine the results of the example above, we see that our system can measure 0 volts, 0.04706 volts, 0.09412 volts (2 * 0.04706 volts), 0.14118 volts (3 * 0.04706 volts), and so on, but it can never represent the voltage 0.02 volts. Its accuracy is not that good. In order to get that accuracy, you would need to increase the number of bits in an integer.
If the voltage range of a 10-bit processor is from a low voltage of 5 volts to a high voltage of 11 volts, what does a binary integer 01100001012 = 389 equal?
Let's begin by finding the voltage per increment over the range. If we find this, we can simply multiply it to our integer value to find the offset from the low voltage of our range.
Voltage increment = (voltage range)/(number of increments)
Voltage increment = (11 volts - 5 volts)/(210 - 1)
Voltage increment = 6 volts/1023 increments
Voltage increment = 0.00587 volts/increment
Multiplying it by the integer value gives us the offset from the low voltage of our range.
offset from bottom of range = 389 * 0.00587 volts/increment
offset from bottom of range = 2.28343 volts
To get the actual voltage represented by the integer, add the offset to the voltage level of the bottom of the range.
voltage represented 389 = 2.28343 volts + 5 volts
voltage represented 389 = 7.28343 volts
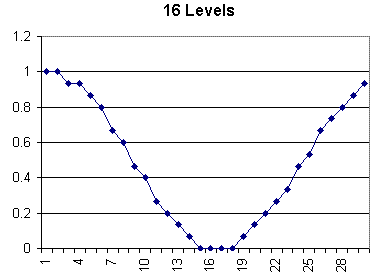
During our discussion of integer representation of analog values, it was mentioned how the number of bits can affect the resolution of the value. In general, an n-bit processor divides the analog range into 2n - 1 intervals. This greatly affects accuracy.
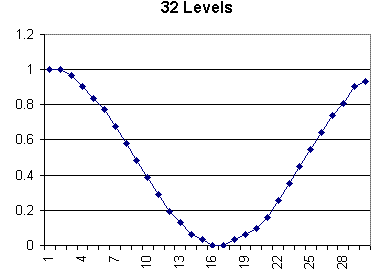
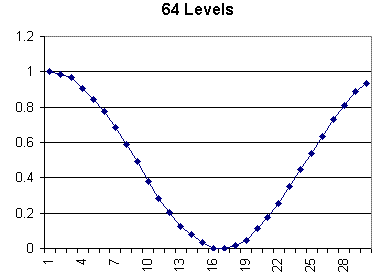
The following six graphs show how the addition of a bit can improve the accuracy of the values represented by the processor's integers.
How Different Bit-Depths Affect Sampling
 |
 |
 |
 |
 |
 |
If an 8-bit processor is set up to measure weight within a range of 0 to 2000 pounds, what is the accuracy?
Just like our earlier example, our range is measured by subtracting the low end from the high end.
range = high value - low value
range = 2000 lbs - 0 lbs
range = 2000 lbs
The number of increments in our range is equal to:
increments = 2n - 1 where n=number of bits
increments = 28 - 1
increments = 255
Therefore, the weight represented by a single increment is:
Increment = (range)/(number of increments)
Increment = 2000 lbs/255
Increment = 7.843 lbs/increment
How can we improve this accuracy using the same number of bits?
Since the only inputs to the equation for accuracy are the number of bits representing an integer and the range, the only thing left to do is reduce the range. Verify what the minimum and maximum values to be measured will be and adjust the range accordingly. For example, if the range were reduced to 500 pounds to 1000 pounds, then the accuracy becomes:
range = high value - low value
range = 1000 lbs - 500 lbs
range = 500 lbs
Increment = (range)/(number of increments)
Increment = 500 lbs/255
Increment = 1.96 lbs/increment
Earlier, I mentioned how a computer can only capture a "snap shot" of an analog voltage. This is sufficient for slowly varying analog values, but if a signal is varying quickly, we may miss details.
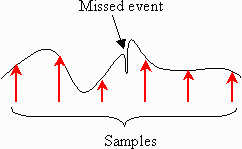
There is also a term called aliasing which is used when a sampling rate is too slow and it misses regular details of a periodic signal.
For example, why aren't fluorescent lights used in sawmills? Plain and simple, fluorescent lights blink much like a very fast strobe light. The blinking is so fast that you might not notice it. (Some people have difficulties not noticing it.)
In a strobe light, objects can appear as if they are not moving. If the frequency of the fluorescent lights and the speed of a moving saw blade are multiples of each other, it can appear as if the blade is not moving.
Another example can be seen when driving at night. The turning wheels of a car in motion under street lights can look like they're moving at a different rate or even backwards.
Both of these examples are situations where aliasing has occurred. Usually, the frequency (turning in the examples given here) is faster than the sampling rate (the blinking lights in the example).
Since a computer sampling an analog signal is like taking a series of snap shots similar to a strobe light flashing for an instant on a object, it must then be possible to lose data between samples.
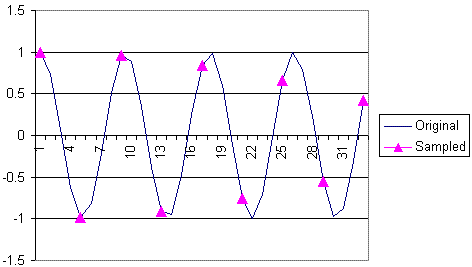
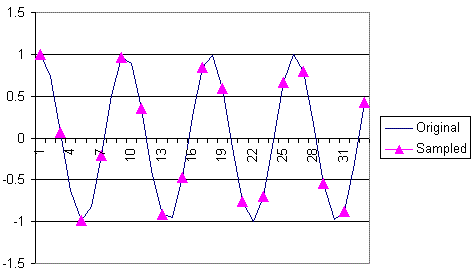
The following three graphs show how different sampling rates can result in different impressions of the signal being watched.
How Different Rates Affect Sampling
 |
 |
 |
Copyright 2003 by David L. Tarnoff. All rights reserved.