Personal Computers (PCs) can be found throughout the modern manufacturing enterprise for some really good reasons. One of the things that makes them so popular and useful is their wicked fast speed; this speed is a direct result of their transistor-based, digital logic design. This same digital logic is used in CNC controllers. To understand the basic care and feeding of CNC controllers, one must know a wee bit about how the data is stored.
The internal storage mechanism of PCs is the electronic flip-flop circuit--a brutally stupid but clever entity that functions like a switch to save data. Not a lot of data, mind you. Just a switch that toggles quickly between being on or being off. On or Off. Zero or One. 0 or 1. It is amazing that those two digits are the heart and soul of the digital computing revolution.
The fundamental building block of digital computers is the little transistorized switch referred to as a "bit" or BInary uniT. The binary part of the definition holds that there are two, and only two, possible values. One bit is not too useful, but modern technology can pack millions--no, billions--of bits into increasingly smaller spaces. So, a nomenclature was developed to help keep track of, as Carl Sagan finally said, these "billions and billions" of bits. Mind you, the computers read and understand only the 0s and 1s; the nomenclature that makes them understandable is for the humans.
As noted, the bit has a value of 0 or 1. If there are two bits, the grouping can have four different values: 00, 01, 10, and 11. If there are three bits in the series, the grouping could be one of eight possible values: 000, 001, 010, 011, 100, 101, 110, and 111. And so on. What should be noted is the geometric progression of possible values: 1 to 2 to 4 to 8. The next item in the series would be 8 times 2 or 16. By arranging the groupings vertically, one can clearly see the progression of the powers of 2:
| Power of 2 | Value |
|---|---|
| 20 | 1 |
| 21 | 2 |
| 22 | 4 |
| 23 | 8 |
| 24 | 16 |
| Etc. | |
By expanding the grouping to 8 bits (called a "byte" as in "bite size chunks" of data...clever, huh?) and reorienting the grouping, placing the least significant digit (20) to the right, one gets the following:
| Powers of 2: | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Adding the eight values ( 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 ) yields a value of 255 or one less than 256 ( 28 ). This makes sense as 255 represents the maximum value one could achieve using all eight bits; the minimum value would be achieved by zeroing our all eight bits giving an additional possible value of zero.
As there could be serious confusion about the value of a character string, say "100101", we will need to specify the type of system used.
By convention, if no base system designator is present, one can assume a number is presented in the decimal system (i.e., using the familiar
Base 10 counting system). If the number is in Base 2 (binary format), the number could be represented using a character "b" either at the front
(e.g., 0b100101) or following the number (e.g., 100101b). In either case, the value of the binary number can be converted into a
Base 10 number by plugging in the digits into the bit order shown above and adding the appropriate powers of 2:
| Powers of 2: | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| Decimal Multiplier: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Binary Value: | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| Decimal Value: | 0 | 0 | 32 | 0 | 0 | 4 | 0 | 1 |
| Decimal Total: | 37 | |||||||
The equivalent mathematical conversion could be shortened to the following:
Note that the leading zeros can be surpressed (i.e., 00100101b is equivalent to 100101b).
Rather quickly, two things became pretty obvious concerning data binary storage: (a) encoding and/or decoding the information contained in long, uninterrupted data strings of 0s and 1s, while easy for a computer, is next to impossible for humans; and (b) some type of communication standard would need to be developed before any type of widespread, reliable communication between data processing equipment is achieved.
The first concern is dealt with by using a third number system, the hexadecimal or Base 16 number system. Four bits (also know
as a "nibble" or half a byte) can yield 16 possible values (0000, 0001, 0002, .... 1110, 1111), hexadecimal or hex notation can
substantially reduce the complexity. The only weird thing about have a base 16 system is that one runs out of numbers after 9.
Therefore, hex notation uses the letters A through F to represent the decimal values ten through fifteen.
| Binary - Hexadecimal - Decimal Conversions | ||||||
|---|---|---|---|---|---|---|
| Binary | Hex | Dec | Binary | Hex | Dec | |
| 0000 | 0 | 0 | 1000 | 8 | 8 | |
| 0001 | 1 | 1 | 1001 | 9 | 9 | |
| 0010 | 2 | 2 | 1010 | A | 10 | |
| 0011 | 3 | 3 | 1011 | B | 11 | |
| 0100 | 4 | 4 | 1100 | C | 12 | |
| 0101 | 5 | 5 | 1101 | D | 13 | |
| 0110 | 6 | 6 | 1110 | E | 14 | |
| 0111 | 7 | 7 | 1111 | F | 15 | |
Note that as with binary notation, hexadecimal base values may be identified by appending the letter 'h' to the end of the number (i.e., 25h equals 100101b equals 37 decimal).
The basic use of hexadecimal notation is typically as shorthand for large binary values; four bits in one alpha-numeric character and eight bits in two alpha-numeric characters. For those persons deeply involved with computers (the poor souls!), hex notation quickly becomes the perferred method of speaking of byte-sized data. Fortunately, the closest most CNC programmers will come to hexadecimal notation is when discussing ASCII characters and physical data storage, as will now begin below...
The second great concern of communications was addressed by Bob Bemer of International Business Machines (IBM) in 1960. An industry-wide group under the American National Standards Institute (ANSI) developed the American Standard Code for Information Interchange (or ASCII) character set which was finalized in 1965.
ASCII is a 7-bit code mapping of control codes, numbers, alphabetical characters (both upper case and lower case), and various punctuation characters into 128 decimal entities (27 = 128). As discussed above, computer data is typically broken into "byte" size chunks of eight bits, so what about that last (eighth) bit? That bit, often referred to as the parity bit, is used for an error identification process that was helpful in the early days of CNC programs where the physical dta storage media could be easily damaged (e.g., torn, ripped, or mutilated). Parity schemes are discussed below.
| ASCII Values (Hexadecimal Format) | |
|---|---|
0 1 2 3 4 5 6 7 8 9 A B C D E F
0 NUL SOH STX ETX EOT ENQ ACK BEL BS HT LF VT FF CR SO SI
1 DLE DC1 DC2 DC3 DC4 NAK SYN ETB CAN EM SUB ESC FS GS RS US
2 SP ! " # $ % & ' ( ) * + , - . /
3 0 1 2 3 4 5 6 7 8 9 : ; < = > ?
4 @ A B C D E F G H I J K L M N O
5 P Q R S T U V W X Y Z [ \ ] ^ _
6 ` a b c d e f g h i j k l m n o
7 p q r s t u v w x y z { | } ~ DEL
|
|
| Legend | |
| Control Codes 00h-1fh | Numbers 20h-29h |
| Upper Case Letters 41h-5Ah | Lower Case Letters 61h-7Ah |
| Punctuation 20h-30h, 5Bh-60h, & 7Bh-7Fh | |
The numbers 0 - 9 are mapped to ASCII 48 - 57 decimal. Why start at 48 decimal? It become obvious if we use hexadecimal notation as the digits map effortlessly into ASCII 30h - 39h. The hexadecimal value of 30 is equal to 110000 binary . By setting the four least most significant digits to represent the values between 0 and 9 (binary 0 through 1001), the numbers can be mapped directly.
The alpha characters (e.g., A - Z and a - z) likewise map into the hexadecimal values 41h - 5Ah for the upper case letters and 61h - 7Ah for the lower case letters. Filling the gaps betwen the control codes, numbers and letters one will find the common punctuation characters. It should be noted that the ASCII character set is quite limited and not very suitable for handling the myriad character sets used throughout the world. For that reason, the ASCII character set has been
extended for DOS and Windows through the use of the eight (or parity) bit and with the use of the
escape [Esc] character.
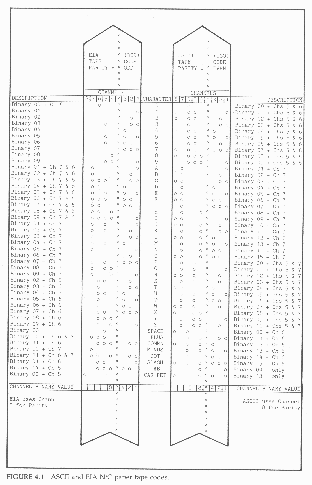In the earlier N/C systems, the most commonly used program storage medium was paper tape. A paper tape is one inch wide. As shown in Figure 4.1, the tape is considered to have eight tracks (called channels) that run along the length of the tape. The channels are numbered 1 through 8 from right to left. Arrays consisting of 1 to 8 holes are punched across the width of the tape. (Small holes between the third and fourth channels are for the tape drive sprocket teeth; they have no symbolic meaning.) Some channels may have a hole in the array; other channels may not. Each of the across-the-tape array of holes is spaced 1/10 inch apart along the length of the tape and corresponds to an alpha character, a numeral, or some other symbol. Which character each array represents is determined by which channels are punched and which are not.
Click inside image to open a much
larger image in a new browser window ->
The first four of the eight channels (right to left) have numerical significance. They are assigned numerical values based on the binary (base 2) number system. The numerical values of channels 1 through 4 are 1, 2, 4, and 8 respectively. Channel 1 has a numerical value of one (2 to the zero power); channel 2 has a numerical value of two (2 to the first power); channel 3 has a numerical value of four (2 to the second power); and channel 4 has a numerical value of eight (2 to the third power).
The numerical value of an array across the tape is the sum total of the value of the channels 1 through 4 in which holes are punched. For example:
| A hole in channel 1 only = 1 A hole in channel 2 only = 2 A hole in channels 1 and 2 = 1 + 2 = 3 A hole in channel 3 only = 4 A hole in channels 1 and 3 = 1 + 4 = 5 A hole in channels 2 and 3 = 2 + 4 = 6 A hole in channels 1, 2, and 3 = 1 + 2 + 4 = 7 A hole in channel 4 only = 8 A hole in channels 1 and 4 = 1 + 8 = 9 A hole in channel 6 only (or 5 and 6) = 0 |
There are two popular code systems in wide use for encoding N/C programs on paper (and magnetic) tape. One code is called the ASCII code (ASCII stands for the American Standard Code for Information Interchange). The ASCII code is also called the RS-358 code and the ISO (International Standards Organization) code. The other code is called the EIA code (EIA stands for the Electronic Industries Association). The EIA code is sometimes called the RS-244 or the BCD (Binary Coded Decimal code, which is a misnomer, as both the EIA and ASCII codes are binary coded decimal).
The numerals 1 through 9 are the same in both the EIA and ASCII codes. Both codes add holes in channels 5, 6, and/or 7 to convert numeral characters to alpha characters and other symbols, but not the same way. The additional hole(s) used is (are) different for the two codes. As shown in Figure 4.1, for example, the EIA code alpha character W consists of the numeral 6, with an additional hole punched in channel 6. The ASCII W is the numeral 7, with additional holes punched in channels 5 and 7. EIA uses channel 8 for only one purpose--to represent the End Of Block (EOB) character. ASCII uses what would be the numeral 13 (channels 1, 3, and 4) for the EOB character. The ASCII code makes provision for both capital and lowercase alpha characters; the EIA code does not provide for lowercase characters. Certain characters, like the percent sign, parentheses, and the colon, exist in the ASCII code but not in the EIA code.
Each code is designed so that every character (array across the tape) in that code will have either an odd number of holes (EIA) or an even number of holes (ASCII). This characteristic is called parity. Initially, each character will have either an even number or an odd number of holes punched, depending on how many punched holes are required for each character.
For example, the numeral 1 requires a hole punched in channel 1, an odd number of holes. The numeral 3 requires holes punched in channels 1 and 2, an even number of holes. The EIA code adds an extra hole (in channel 5) to all characters having an even number of holes. With this extra hole added to the even-hole characters, all EIA characters then have an odd number of holes. This is called odd parity. The ASCII code adds an extra hole (in channel 8) to all characters having an odd number of holes. With this extra hole added to the odd-hole characters, all ASCII characters then have an even number of holes. This is called even parity.
The reason for having parity is that it is possible for a tape punch to miss punching a hole in an array. This would change the parity of that character from odd to even or vice versa. It would also change the meaning of that array to some other character, possibly making the entire program fail. The N/C controller, set to accept either EIA or ASCII characters, will expect each ASCII or EIA character to have its certain parity. If it finds a character with the wrong parity (called a parity error), it knows something is wrong and it stops dead in its tracks! It is then up to the programmer to examine the tape (by running it through a tape reader/printer) and correct the error.
It is not necessary for an N/C programmer to be able to directly read the ASCII or EIA characters punched on a paper tape. Electronic/mechanical tape readers do that. However, in order to read an existing tape into a microprocessor for editing, it may be necessary to set the system to read the particular code used on the tape. A system that receives ASCII coded characters when it is set to expect EIA characters may have a nervous breakdown. Therefore, the programmer must be able to examine a punched tape and determine whether the code is ASCII or EIA. This is done by simply counting the holes in several arrays. If the number in all arrays is an even number, the code is ASCII; if all the arrays are odd parity, the code is EIA.
| Next: Hardware |
|---|
Back to Contents Page
Updated Jan. 18, 2002
Copyright © 1988, 2002 by George Stanton and
Bill Hemphill
All Rights Reserved