


Next: Chapter 04
Up: Chapter 03
Previous: Review
- #02
-
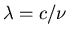 , with
, with
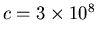 m/s and
m/s and 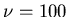 MHz
(or
MHz
(or 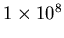 Hz), the wavelength of FM 100 is 3 m.
Hz), the wavelength of FM 100 is 3 m.
- #06
- Object A is hotter. Wien's Law is that
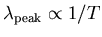 , so the ratio of temperatures is
, so the ratio of temperatures is
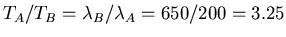 . Stefan's Law is that the rate of energy
emitted from a unit of area goes as
. Stefan's Law is that the rate of energy
emitted from a unit of area goes as 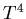 , and so object A radiates
, and so object A radiates
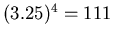 times more energy per second than object B.
times more energy per second than object B.
- #09
- This is a proportions problem, similar to the previous
problem. Using Wien's Law, we have that
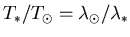 . Solving for the protostar peak wavelength
. Solving for the protostar peak wavelength 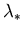 by
cross-multiplying, we have that
by
cross-multiplying, we have that
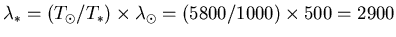 nm, or 29,000 Å, far in the infrared.
nm, or 29,000 Å, far in the infrared.
- #13
- A Doppler shift problem. The signal is 100 MHz, but you
want to receive it at 99 MHz. That is a drop in frequency by 1 MHz
out of 100 MHz, or 1%. This is normally called a redshift (recall,
a drop in frequency is an increase in wavelength). The spacecraft would
have to be moving away from the Earth. The speed
 is given by
is given by
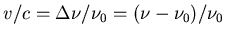 , where
, where 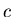 is the speed of
light,
is the speed of
light, 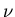 is the measured frequency, and
is the measured frequency, and 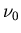 is the original
emitted frequency. Keeping frequencies in MHz, and using
is the original
emitted frequency. Keeping frequencies in MHz, and using  km/s,
the spacecraft must move away from the Earth at
km/s,
the spacecraft must move away from the Earth at
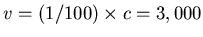 km/s. (That converts to almost 11 million km per hr!)
km/s. (That converts to almost 11 million km per hr!)



Next: Chapter 04
Up: Chapter 03
Previous: Review
Rico Ignace
2004-09-10