3. 2-Manifolds

Inspired by E.A. Abbott's Flatland (1884), we often talk about the shape of the universe by ignoring one of the spatial dimensions and imagining ourselves to be 2-dimensional. This gives us the ability to "stand back" and get an external view of this 2-D universe. We should be careful with this analogy, though. Of course there is no meaning to the idea of getting "out of the universe" and looking back down at it! This brings us to the idea of intrinsic and extrinisic properties of a manifold. An intrinsic property of a manifold is a property that can be determined from within the manifold. An extrinsic property of a manifold is a property that can only be determined by stepping out of the manifold and viewing the way in which it is embedded in a higher dimensional space. Therefore, the only properties of our universe which have empirical meaning are those which are intrinsic.

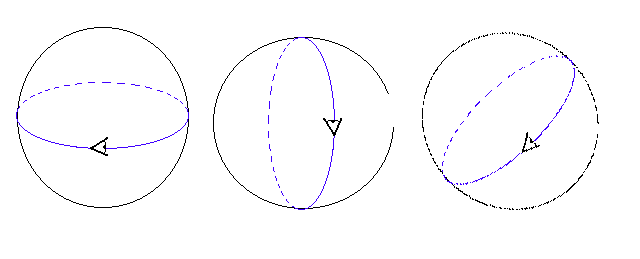
First, lets consider what the inhabitants of a 2-sphere "see." This space has positive curvature at all points and therefore the (local) geometry is spherical. The (global) topology is determined by following the paths of photons. Photons follow great circles on the sphere (that is, geodesics are great circles). Therefore an inhabitant of this universe sees distant images of himself in all directions. See Figure 4. This property is sufficient to tell the inhabitant that his universe is topologically equivalent to the 2-sphere.

Next, lets consider 2-manifolds that are tori. In a doughnut shaped universe, there are two fundamental directions in which an inhabitant can look and "see himself." See Figure 5. In certain other directions, the inhabitant can see himself as well, but these other directions are combinations of the two fundamental ones (a photon can spiral around through the hole of the doughnut an integer number of times while at the same time going around the hole an integer number of times, before returning to its point of origin). An inhabitant of this type of universe would conclude that it has topological properties different from the 2-sphere. It also has different geometric properties. In some regions, the surface has positive curvature and spherical geometry. In other regions, it has negative curvature and hyperbolic geometry.

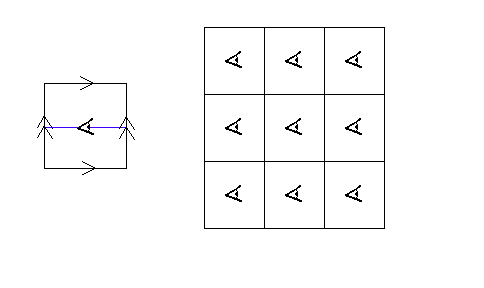
Another example of a 2-manifold is the flat 2-torus. It can be thought of by starting with a square and "conceptually" joining opposite edges as shown in Figure 6a. As an inhabitant travels off the left "edge," he reappears at the right "edge." Of course, the edges are artificial and the inhabitant simply sees a space tiled with copies of the square (called the fundamental domain) and of himself. See Figure 6b. This manifold is topologically equivalent to the torus of Figure 5. However, it is everywhere flat and has Euclidean geometry.

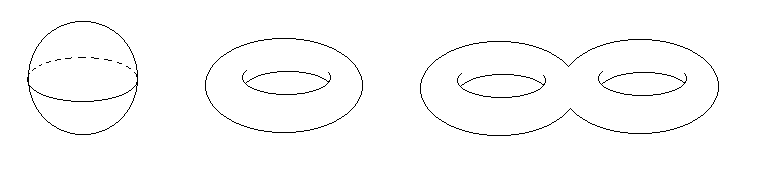
If we wish to classify surfaces, then we will break them into topologically distinct classes. There are two general classes of manifolds: orientable and nonorientable. In this presentation, we restrict ourselves to orientable manifolds. It was discovered around 1900 by mathematicians that every finite orientable 2-manifold is either the 2-sphere, or a collection of tori "glued together." The number of "holes" in the manifold (called the genus) determines the surface. For example, a 2-sphere is a surface of genus 0 and a torus is a surface of genus 1. Figure 7 gives surfaces of genus 0, 1, and 2.

Figure 4. An inhabitant of the 2-sphere universe sees the back of his own head, regardless of the direction in which he looks.

Figure 5. In a 2 dimensional toroidal universe, there are two fundamental directions in which an inhabitant can look to see the back of his own head. The inhabitant can also look in a direction which spirals around the hole and see the back of his own head (such a direction is, in a sense, a combination of the two fundamental ones). The fact that there are directions an inhabitant can look and not see the back of his own head gives an empirical way for the inhabitant to distinguish this universe from the 2-sphere universe.

Figure 6. (a) The flat 2-torus is formed by conceptually joining the opposite edges of a square, as indicated by the arrows. When an inhabitant looks to the right, he sees the back of his own head. (b) In fact, the inhabitant sees the whole plane tiled with images of himself. The grid of lines simply reflects the multiple images of the fundamental domain, and has no physical significance.

Figure 7. Every finite orientable 2-manifold can be classified according to its genus. Here are such manifolds of genus 0 (the 2-sphere), genus 1 (the torus), and genus 2 (two "Siamese tori"). In general, an orientable surface of genus n consists of n tori glued together.

Go to Section 4.