The formal definition of a manifold can be quite cumbersome and beyond the reach of most undergraduates. However, informal definitions of 2- and 3-manifolds can be used in our discussion with little loss (many of our "informal definitions" are from Weeks 1985). A 2-manifold (also called a surface) is a space which is locally 2-dimensional. A 3-manifold is a space which is locally 3-dimensional. Strictly speaking, a manifold does not have an edge (or boundary). Therefore the surface of a sphere is a 2-manifold (called the 2-sphere), but the interior of a sphere is not a manifold, since it has a boundary. From here on, we restrict our attention to 2- and 3-manifolds. We will concentrate on 2-manifolds when we are trying to visualize things clearly, and we will concentrate on 3-manifolds when we consider the shape of our universe, since our universe is 3 dimensional.
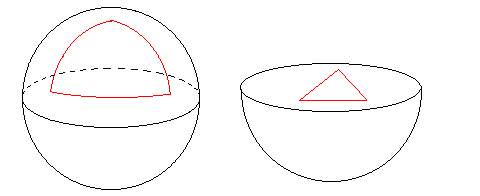
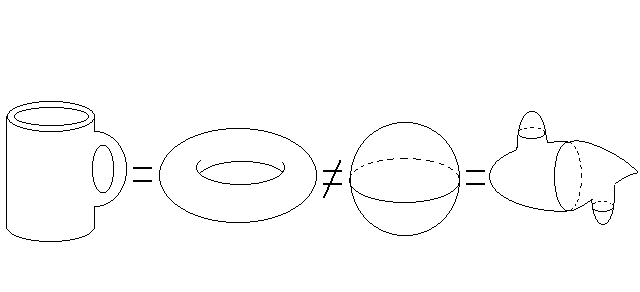
The properties of a manifold that do not change under continuous deformations make up the manifold's topology. For example, connectedness is a topological property. See Figure 2. The properties of a manifold that do change under continuous deformations make up a manifold's geometry. For example, curvature, area, distance, and angles are geometric properties. See Figure 3. Again informally, a local property of a manifold is one which is observable in a small region of the manifold (such as the type of geometry). A global property of a manifold is one which requires consideration of the manifold as a whole to determine (such as the type of connectedness of the manifold). We will give classifications of 2- and 3-manifolds according to their global topology. The question we wish to address can be worded as: "What is the global topology of the universe?"