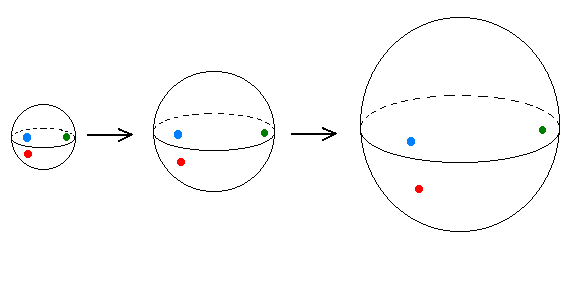
In the popular literature, the big bang is often portrayed as an explosion of matter and energy which is thrown out from a central point into existing space. This is inaccurate, and a better metaphor for the big bang is the (locally) two dimensional analogy of an inflating balloon. If we imagine ourselves as two dimensional creatures living {\it within the surface} of a sphere which expands with time, then our pretend universe has several desirable (empirical) properties: (1) it has no edge, (2) it has no center, and (3) if the sphere inflates uniformly, then Hubble's Law is obeyed. See Figure 1. The model universe has a geometry in which the sums of the measures of the angles of a triangle is greater than 180o (a version of noneuclidean geometry called spherical geometry). The curvature of this universe is positive. It also has the property that a photon traveling in a "straight line" (or more accurately, on a geodesic) will eventually return to its source (assuming an expansion sufficiently slow in comparison with the speed of light). Therefore, inhabitants of this universe can see distant images of themselves! This peculiar optical property results from the global topology of our pretend universe. With this model as a starting point, we will present an introduction to the topology of 2- and 3-manifolds. From this discussion, we will give examples of possible universes which are closed, yet still have zero or negative curvature (a possibility which is often overlooked in undergraduate classes). Finally, empirical methods for potentially answering the question "What is the shape of our universe?" will be described.
