THE SHAPE OF SPACE
6. The 3-Torus
The simplest example of a finite 3-dimensional surface (generally called a
3-manifold) is the 3-torus. It can be constructed
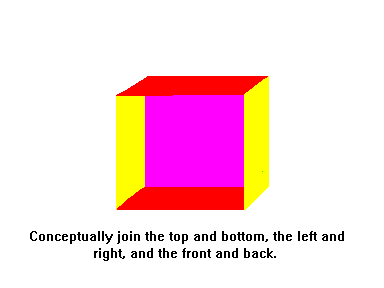
by starting with a cube
(called the fundamental domain of the 3-torus) and
then conceptually joining opposite faces.
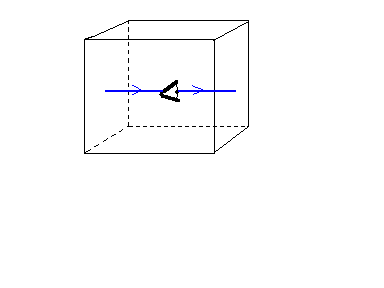
 In such a space, an object which travels out to the left hand side of the
cube instantly reappears at the right hand side (and similar for the
top-bottom and the front-back). Therefore if we lived in such a universe,
we could look to the right (or left) and see the back of our own head. We
could also look straight up (or down), or straight out the front (or back)
of the cube and see ourselves.
In such a space, an object which travels out to the left hand side of the
cube instantly reappears at the right hand side (and similar for the
top-bottom and the front-back). Therefore if we lived in such a universe,
we could look to the right (or left) and see the back of our own head. We
could also look straight up (or down), or straight out the front (or back)
of the cube and see ourselves.
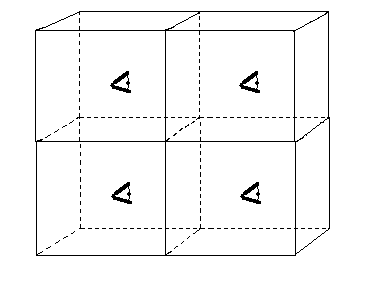
 In fact, if we live in such a space, we would see an entire grid of copies
of ourselves throughout the space.
In fact, if we live in such a space, we would see an entire grid of copies
of ourselves throughout the space.
 This space is flat (that is, it has Euclidean geometry and zero curvature)
and finite. If this manifold is the shape of our universe, then we can
imagine the big bang as the point at which a 3-torus started expanding. As
time goes by, this 3-torus continues to expand. Since this manifold is
flat, in this model the universe continues to expand forever (but just
barely). This model illustrates that we can have the philosophically
desirable property of a finite universe, even though the universe is "open"
and will continue to expand forever.
This space is flat (that is, it has Euclidean geometry and zero curvature)
and finite. If this manifold is the shape of our universe, then we can
imagine the big bang as the point at which a 3-torus started expanding. As
time goes by, this 3-torus continues to expand. Since this manifold is
flat, in this model the universe continues to expand forever (but just
barely). This model illustrates that we can have the philosophically
desirable property of a finite universe, even though the universe is "open"
and will continue to expand forever.
It is also possible to have a finite universe which is negatively curved.
in making such a space, opposite faces of a dodecahedron are conceptually
joined. The resulting manifold is called the
Seifert-Weber manifold and has negative curvature.
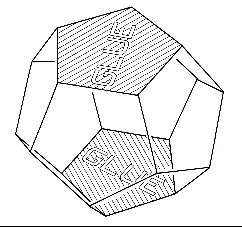
(From The Shape of Space by J. Weeks [reference 3].)
Goto Section 7.




