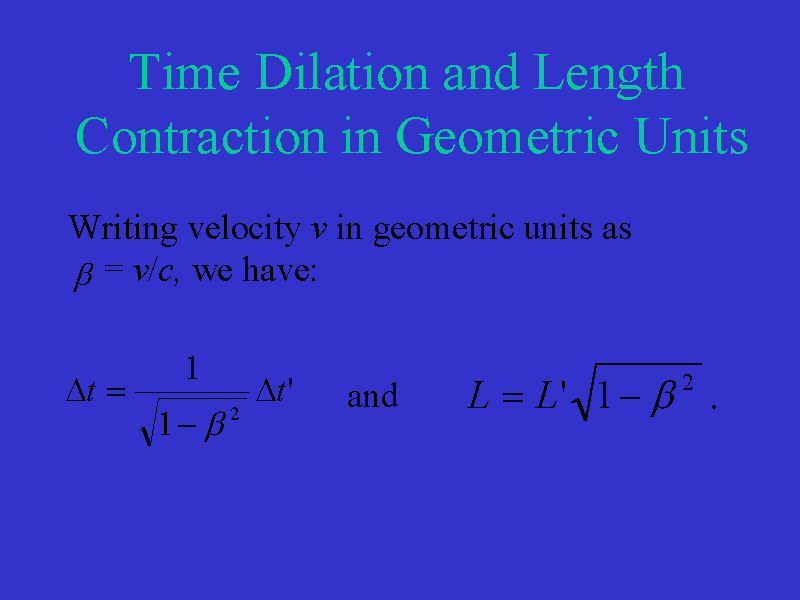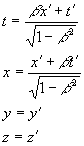Relativity and Black Holes
Spacetime and the Interval
 In 3-dimensional geometry, positions are represented by points
(x,y,z).
In physics, we are interested in events which have both time and
position: (t,x,y,z). The collection of all possible events is called
spacetime.
In 3-dimensional geometry, positions are represented by points
(x,y,z).
In physics, we are interested in events which have both time and
position: (t,x,y,z). The collection of all possible events is called
spacetime.
 With an event (t,x,y,z) in spacetime we associate the
units of cm with coordinates x, y, z. In addition, we express time
t
in terms of cm by multiplying it by the speed of light.
(In fact, many texts use
coordinates (ct, x, y, z) for events.) These common units (cm for us)
are called geometric units. We express
velocities in dimensionless units by dividing them
by c. So for velocity v (in cm/sec, say) we associate the
dimensionless velocity
With an event (t,x,y,z) in spacetime we associate the
units of cm with coordinates x, y, z. In addition, we express time
t
in terms of cm by multiplying it by the speed of light.
(In fact, many texts use
coordinates (ct, x, y, z) for events.) These common units (cm for us)
are called geometric units. We express
velocities in dimensionless units by dividing them
by c. So for velocity v (in cm/sec, say) we associate the
dimensionless velocity 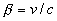 .
Notice that under this convention,
the speed of light is 1.
.
Notice that under this convention,
the speed of light is 1.
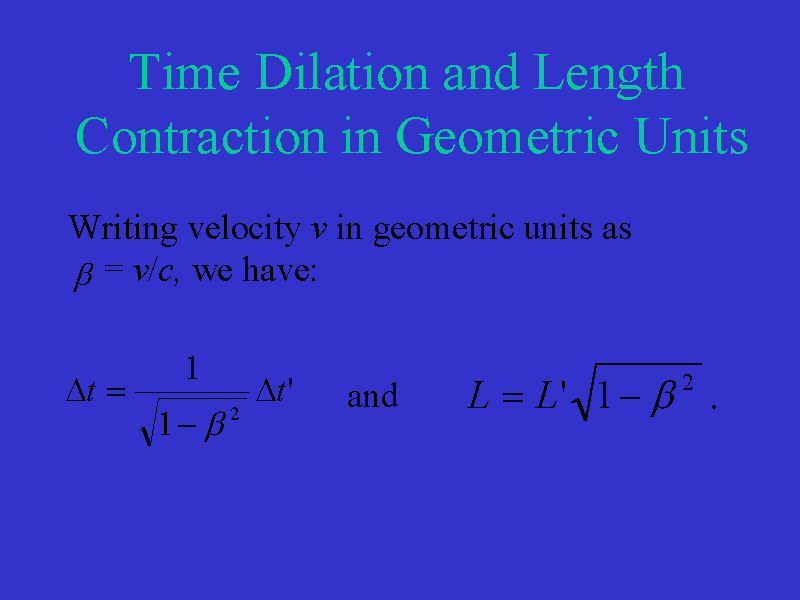 This leads us to restate time dilation and length
contraction as:
This leads us to restate time dilation and length
contraction as:
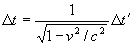 and
and

The concept of spacetime was introduced by Hermann Minkowski.
 Minkowski, in fact, was one of Albert Einstein's mathematics
professors at the Zurich Politechnikum in 1900. Einstein's lack of respect
for authority and his casual attitude toward coursework caused Minkowski to
label Einstein a "lazy dog"... certainly an incorrect assessment!
Minkowski, in fact, was one of Albert Einstein's mathematics
professors at the Zurich Politechnikum in 1900. Einstein's lack of respect
for authority and his casual attitude toward coursework caused Minkowski to
label Einstein a "lazy dog"... certainly an incorrect assessment!
 In Gottingen, Minkowski studied Einstein's
1905 paper on special relativity and was
impressed. This study lead Minkowski to his formulation of an absolute
four-dimensional spacetime.
In Gottingen, Minkowski studied Einstein's
1905 paper on special relativity and was
impressed. This study lead Minkowski to his formulation of an absolute
four-dimensional spacetime.
In an address to the 80th Assembly of German Natural Scientists and
Physicians at Cologne in September 1908, Minkowski opened with this
statement:

When Einstein learned of Minkowski's work, he was not impressed. To
Einstein, Minkowski was merely rewriting the laws of special relativity in
a new mathematical language. Einstein felt that the abstract mathematics
obscured the underlying physics. However, we will soon see that Einstein
had to change his mind about the usefulness of spacetime.
 As a sad footnote, Hermann Minkowski died of appendicitis in 1909 at the age
of 45. This was just a matter of months after his address in Cologne.
Minkowski is honored today by the fact that his spacetime is often called
Minkowski spacetime or the Minkowski vector space.
As a sad footnote, Hermann Minkowski died of appendicitis in 1909 at the age
of 45. This was just a matter of months after his address in Cologne.
Minkowski is honored today by the fact that his spacetime is often called
Minkowski spacetime or the Minkowski vector space.
Let's explore the structure of this Minkowski spacetime.
 Suppose events A and B occur in inertial frame S at
(t1, x1, y1,
z1) and (t2, x2,
y2, z2), respectively.
Then define the interval (or proper
time) between A and B as the possibly imaginary quantity
Suppose events A and B occur in inertial frame S at
(t1, x1, y1,
z1) and (t2, x2,
y2, z2), respectively.
Then define the interval (or proper
time) between A and B as the possibly imaginary quantity
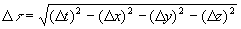 where
where 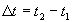 ,
, 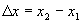 ,
and so forth. Notice that the interval squared
is simply the difference of
time separation squared and spatial separation squared.
,
and so forth. Notice that the interval squared
is simply the difference of
time separation squared and spatial separation squared.
 We have seen that measurements of time
and space are relative to the inertial frame in which an observer
makes the measurements.
However, it can be shown that the interval between two events is the
same,
regardless of the inertial frame of an observer. That is, the
INTERVAL IS AN ABSOLUTE
in Minkowski spacetime! The interval is to
spacetime geometry what the distance is to Euclidean geometry. So, in a
real sense, the special theory of relativity is misnamed. It is
actually a theory of an absolute. Though the familiar quantities of time
and distance are relative, the interval is an absolute quantity (or better yet, an
invariant quantity).
We have seen that measurements of time
and space are relative to the inertial frame in which an observer
makes the measurements.
However, it can be shown that the interval between two events is the
same,
regardless of the inertial frame of an observer. That is, the
INTERVAL IS AN ABSOLUTE
in Minkowski spacetime! The interval is to
spacetime geometry what the distance is to Euclidean geometry. So, in a
real sense, the special theory of relativity is misnamed. It is
actually a theory of an absolute. Though the familiar quantities of time
and distance are relative, the interval is an absolute quantity (or better yet, an
invariant quantity).
 An interval in which time separation dominates and
An interval in which time separation dominates and
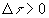 is called timelike.
An interval in which space
separation dominates and
is called timelike.
An interval in which space
separation dominates and 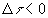 is called spacelike. An
interval for which
is called spacelike. An
interval for which 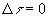 is called lightlike.
A single photon can be present at two events which are separated by a lightlike
interval.
is called lightlike.
A single photon can be present at two events which are separated by a lightlike
interval.
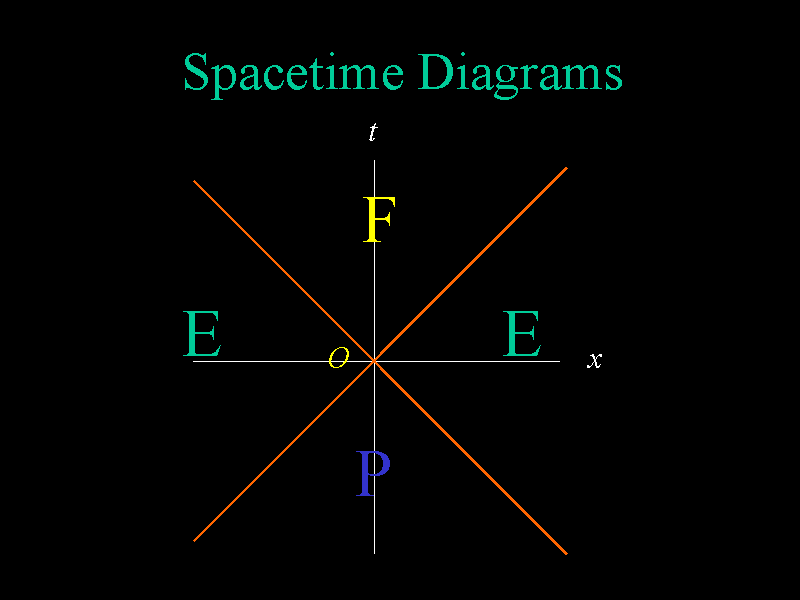 If we have a pair of axes, one of which represents space (the x-axis) and
one of which represents time (the t-axis), then we can discuss spacetime
diagrams. We can use the origin O to partition this two dimensional
spacetime into several sets using the interval between event O and the
other events in the plane. If the interval between O and an event is
timelike, then the event will lie either in region F or region
P.
Region F consists of the "future events for O."
Region P consists
of the "past events for O." The boundary of these regions (here in red) is the
collection of events separated from O by a lightlike interval. The
events in region E are separated from O by a spacelike interval. The
events in region F are those that event O can influence. The
events in region P are the events which can influence event
O. The
events in region E are too far from event O to either be influenced by
O or to influence O. That is, there isn't enough time for anything
(not even photons) to be present at both event O and an event in region
E. For this reason, there are certain causality
restrictions between the different events in this spacetime.
If someone were to shine a flashlight at O then the wavefront would
travel out along the boundary between region F and region
E. Notice
that the slopes of these lines are ±1. This is because, in geometric
units, the speed of light is 1.
If we have a pair of axes, one of which represents space (the x-axis) and
one of which represents time (the t-axis), then we can discuss spacetime
diagrams. We can use the origin O to partition this two dimensional
spacetime into several sets using the interval between event O and the
other events in the plane. If the interval between O and an event is
timelike, then the event will lie either in region F or region
P.
Region F consists of the "future events for O."
Region P consists
of the "past events for O." The boundary of these regions (here in red) is the
collection of events separated from O by a lightlike interval. The
events in region E are separated from O by a spacelike interval. The
events in region F are those that event O can influence. The
events in region P are the events which can influence event
O. The
events in region E are too far from event O to either be influenced by
O or to influence O. That is, there isn't enough time for anything
(not even photons) to be present at both event O and an event in region
E. For this reason, there are certain causality
restrictions between the different events in this spacetime.
If someone were to shine a flashlight at O then the wavefront would
travel out along the boundary between region F and region
E. Notice
that the slopes of these lines are ±1. This is because, in geometric
units, the speed of light is 1.
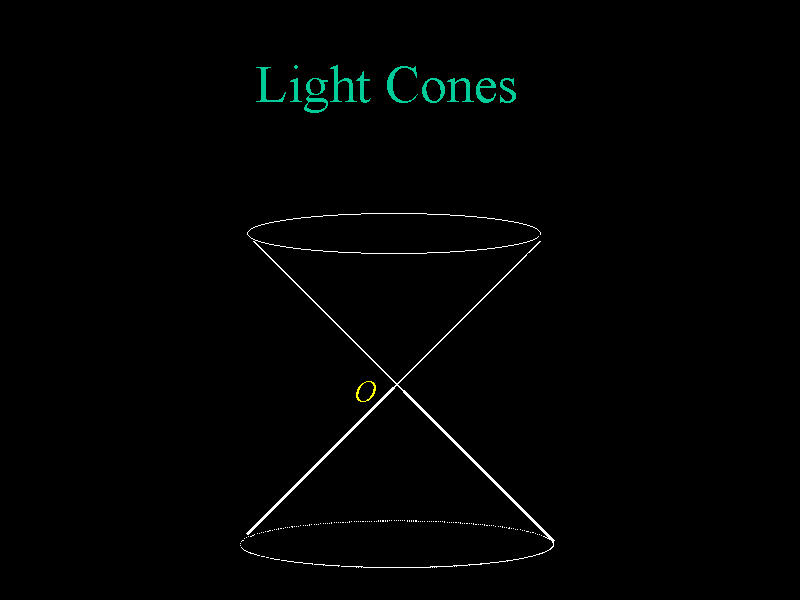
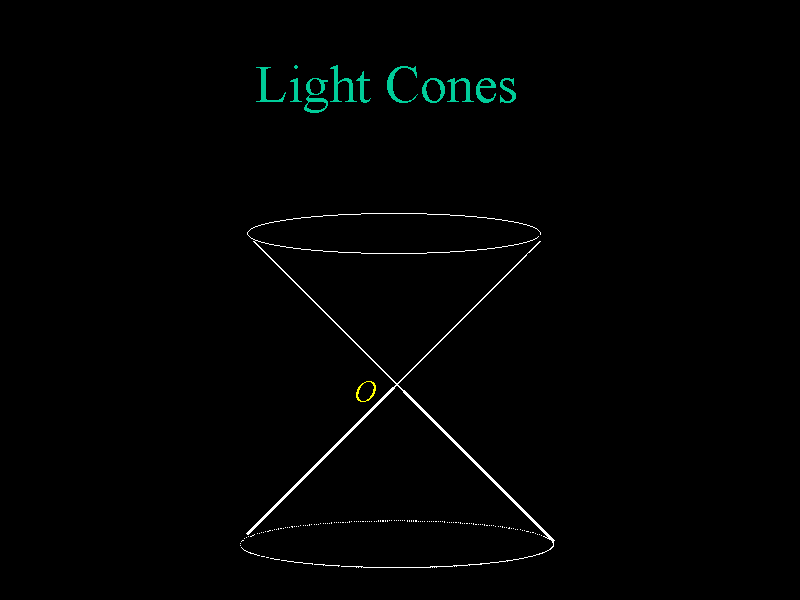 We can introduce a second spatial axis and use spacetime diagrams to create
light cones for given events. Here, the upper cone is the
future light cone of the event at point O. The
lower cone is the past light cone of event O.
The surface of the
lower lightcone is the collection of events which an observer at O can
see, and the surface of the upper lightcone are events at which an observer
could see event O.
We can introduce a second spatial axis and use spacetime diagrams to create
light cones for given events. Here, the upper cone is the
future light cone of the event at point O. The
lower cone is the past light cone of event O.
The surface of the
lower lightcone is the collection of events which an observer at O can
see, and the surface of the upper lightcone are events at which an observer
could see event O.
 If S and S' are inertial frames with S' moving relative
to S with velocity v as shown here, then the coordinates of
a given event which has
coordinates (t,x,y,z) in the S frame and coordinates
(t', x', y', z') in the S' frame will satisfy the
equations:
If S and S' are inertial frames with S' moving relative
to S with velocity v as shown here, then the coordinates of
a given event which has
coordinates (t,x,y,z) in the S frame and coordinates
(t', x', y', z') in the S' frame will satisfy the
equations:
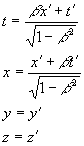 This collection of equations is called the Lorentz Transformation.
We can verify that the interval between two events is fixed under the
Lorentz transformation.
This collection of equations is called the Lorentz Transformation.
We can verify that the interval between two events is fixed under the
Lorentz transformation.
Go to next section.