Sound waves need a medium though which to travel.
In 1864 James Clerk Maxwell showed that light is an electromagnetic wave. Therefore it was assumed that there is an ether which propagates light waves. The ether was assumed to be everywhere and unaffected by matter. It could be used to determine an absolute reference frame.
In 1881 Albert Michelson performed an experiment (latter repeated by Edward Morley in 1887) to see if he could detect the presence of the ether. This is the classical Michelson-Morley experiment.
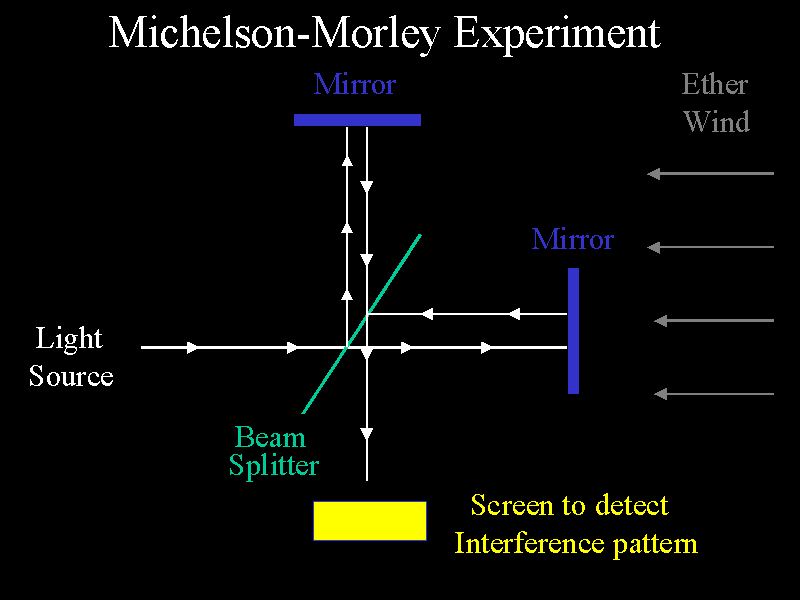
The Michelson-Morley experiment was performed to detect the Earth's motion through the ether. As seen here, the screen will show that the two beams of light which have traveled along different arms display some interference pattern. Since the object contains a beam splitter, some of the photons will travel along one path through the instrument, and other photons will take a different path. This will produce a particular interference pattern on the display screen. If the system is rotated, then the influence of the "ether wind" should change the time the beams of light take to travel along the arms and therefore should change the interference pattern. The experiment was performed at different times of the day and of the year. NO CHANGE IN THE INTERFERENCE PATTERN WAS OBSERVED!
In 1892, Fitzgerald proposed that an object moving through the ether wind
with velocity v experiences a contraction in the direction of the
ether wind of 
.
That is, the arm labeled
"arm one" is reduced from it's original length L1 to a new
length 
.
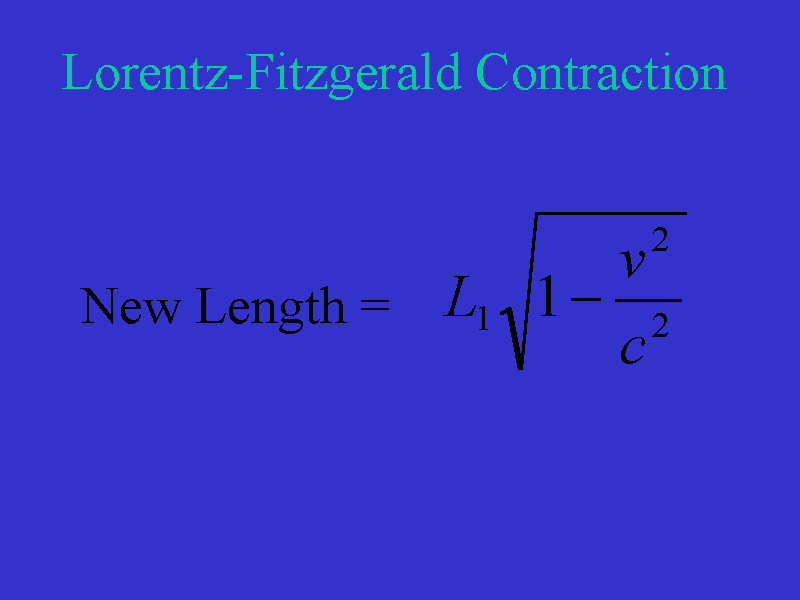
This is called the Lorentz-Fitzgerald contraction and has the potential to explain the negative result of the Michelson-Morley experiment.
However, even under this assumption of contraction due to the ether wind, a Michelson-Morley apparatus with unequal arms will exhibit a pattern shift over a 6 month period as the Earth changes direction in its orbit around the Sun. In 1932, Kennedy and Thorndike performed such an experiment and detected no such shift.
The implication of these experiments is that the speed of light is constant and the same in all directions for all observers.
A frame of reference is a system of spatial coordinates and possibly a temporal coordinate. A frame of reference in which the Law of Inertia holds is an inertial frame or inertial system. An observer at rest (that is, with zero velocity) in such a system is an inertial observer.
Special relativity deals with the observations of phenomena by inertial observers and with the comparison of observations of inertial observers in equivalent frames (that is, NO ACCELERATION!). It is general relativity which takes into consideration the effects of acceleration (and therefore gravitation) on observations.
Albert Einstein published "Zur Elektrodynamik bewegter Korper" (On the Electrodynamics of Moving Bodies) in Annalen der Physik (Annals of Physics) volume 17 in 1905. In this paper, he established the SPECIAL THEORY OF RELATIVITY! Quoting from the introduction to this important paper:
In short, we have the following two Postulates of Relativity.
Suppose inertial frame S' moves with velocity v relative to
inertial frame S, as shown here.
Let 
be the time between two events as
measured in the S frame and let 
be the time between the
same two events as measured in the S' frame. An observer in the
S frame sees these quantities related by the equation
and therefore the time interval
is lengthened (or dilated).
Under the same motions of inertial frames, let
.
and therefore distances are shortened (or
contracted).
What's the punch line here?
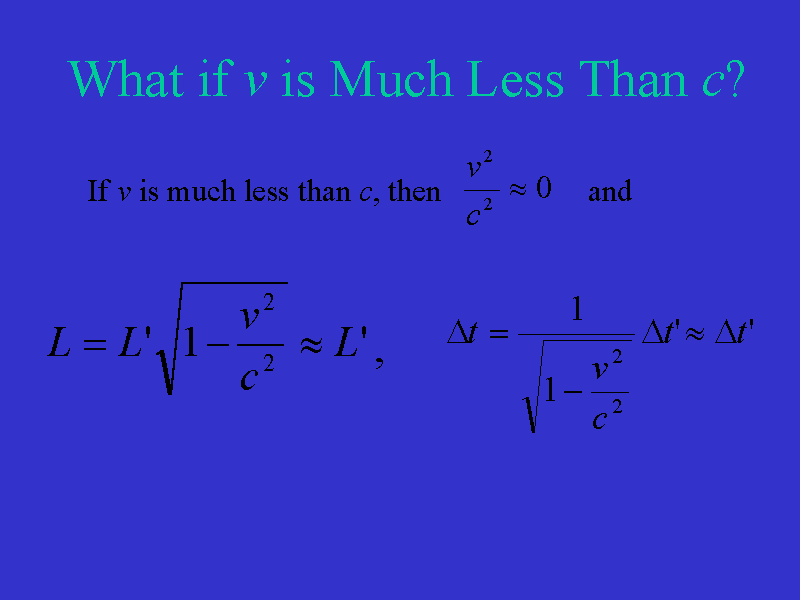
If v is much less than the speed of light, then
L is approximately the same as L' and
is approximately the same as .
Therefore the effects of relativity are not significant
except at speeds near the speed of light. This is the reason we don't
notice relativistic effects in our everyday life.
Go to next section.