AN EXAMPLE OF A STATISTICAL TEST


From: http://www.dvdbeaver.com/film2/DVDReviews33/3_stooges_collection_vol._1.htm
We have no (stated) reason to suspect that there is a difference between the amount of Moe-instituted violence towards Curly versus the amount of Moe-instituted violence towards Shemp. For the sake of illustration, we test a null hypothesis concerning this.

Since we have no reason to suspect a difference between the amount of violence from Moe to Curly or from Moe to Shemp, we test for a difference and perform a two-tailed test. This gives the following null and alternative hypotheses:
H0: "The average number of violent acts by Moe against Curly per episode is the same as the average number of violent acts by Moe against Shemp."
Ha: "The average number of violent acts by Moe against Curly per episode is different than the average number of violent acts by Moe against Shemp."

Five randomly selected Shemp episodes and five randomly selected Curly episodes were chosen. The number of acts of violence by Moe to these Stooges is as follows:

Shemp
Curly
Episode (number)
# of Acts
Shivering Sherlocks (104)
13
Love at First Bite (123)
20
Three Arabian Nuts (129)
9
Cuckoo on a Choo Choo (143)
16
Knutzy Knights (156)
8
Episode (number)
# of Acts
Back to the Woods (23)
12
Three Missing Links (34)
9
An Ache in Every Stake (57)
6
Sock-a-Bye Baby (66)
10
A Bird in the Head (89)
11
Average: x1 = 13.2
Average: x2 = 9.6

The sample standard deviation, s, of a sample of size n is:

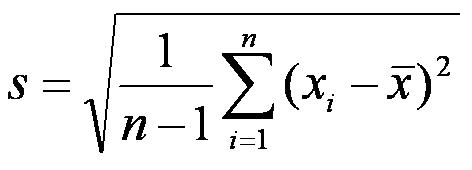
This yields the following sample standard deviations and variances from our data:
Shemp
s1 = 4.9670, s12 = 24.7
Shemp
s1 = 2.3022, s12 = 5.3

The two sample t-test assumes that samples are taken from a normal distribution. Given the means and standard deviations of our samples, this is a reasonable assumption. The t statistic for this data is calculated as:

From the above data, we have:
t = 1.470

Since we have no reason to suspect a difference between the amount of violence from Moe to Curly or from Moe to Shemp, we test for a difference and perform a two-tailed test with t = 1.470.

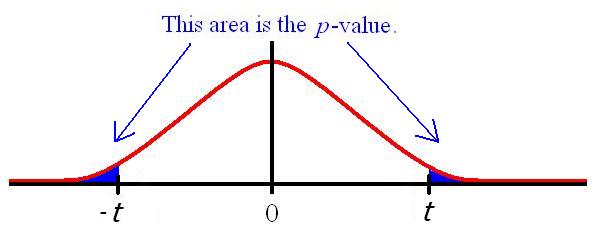
Excel gives a p-value for this data of:

p = 0.1920.
This means that we could reject the null hypothesis, but only with confidence
( 1 - p ) x 100% = 80.80%.

Conclusion?

From: http://www.nndb.com/people/972/000047831/
A level of confidence of 81% is generally considered insufficient (with the "industry standard" level of confidence set at a minimum of 95%). This means that should fail to reject the null hypothesis that the means are the same. This does not mean that we accept the null hypothesis, but that we find the data insufficient to give a conclusive decision.

Go to the next section.

Return to The Three Stooges Statistics webpage.