Part 3: Parametrizations of Circles   

Suppose we are given a circle with radius R centered at a point ( p,q) :

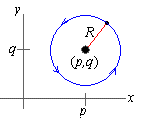
The standard parametrization of such a circle with counterclockwise orientation is given by

EXAMPLE 6    What is the standard parametrization of a circle with radius 1 centered at ( 0,1) ?      

Solution: Substituting p = 0, q = 1, and R = 1 into (2) yields

r( q) = á cos( q),1+sin( q) ñ

To verify this, notice that x = cos( q) and y = 1+sin( q) implies that

x2+( y-1) 2 = cos2( q) +sin2(q) = 1

Notice that example 5 and example 6 are parametrizations of the same curve, thus demonstrating that parametrizations are not unique. Indeed, in applications, the speed at which the circle is being traversed is often important information.

Specifically, if an object is moving in a circle with a constant angular speed w in radians per second, then q = wt. Thus, the path of an object moving in a circle of radius R centered at (p,q) with a constant angular velocity w is parametrized by

r( t) = á p+Rcos( wt),q+Rsin( wt) ñ

It then follows that the circle centered at ( p,q) with radius R has a different parametrization for every possible value of w.       

EXAMPLE 7    Two objects are moving on a circle with radius 2 centered at ( 3,4) . The first is moving at an angular speed of w = 2 radians per second while the second is moving at an angular speed of w = 3 radians per second. Parametrize the motion of each object and compare the two.       

Solution: If we denote the two motions by r₁(t) and r₂( t) , respectively, then

r1( t) = á 3+2cos( 2t),4+2sin( 2t) ñ r2( t) = á 3+2cos( 3t),4+2sin( 3t) ñ

Moreover the second object will traverse the circle 3 times for every 2 traversals of the circle by the first object. Indeed, r₁(t) and r₂(t) are shown below for ever increasing values of t.

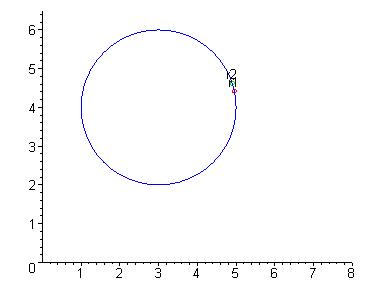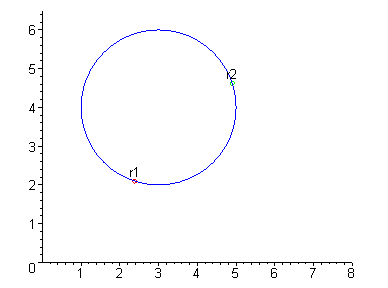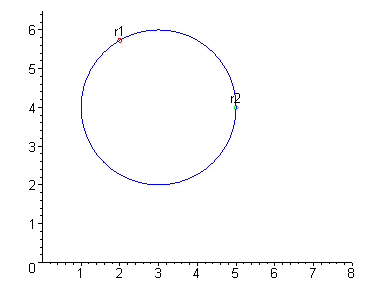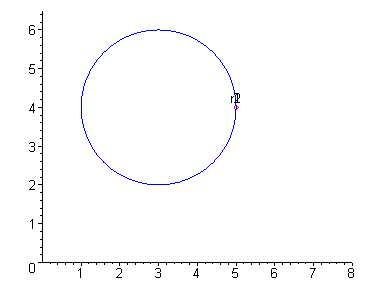click to toggle animation