Part 3:  The Decomposition of Acceleration   

If we now combine (1), (2), and (5), then we find that the acceleration of a curve parameterized by r( t) is

a = dv dt T+kv2N

(6)

The quantity a_T = dv/dt is the rate of change of the speed and is often called the linear acceleration for the parameterization. The linear acceleration is also known as the tangential component of acceleration because it measures the acceleration in the direction of the velocity.

The quantity a_N = kv² is called the normal component of acceleration because it measures the acceleration applied at a right angle to the velocity. Since by definition,

k =  dq ds  =  dq dt dt ds  =  1 v dq dt

the normal component of acceleration can also be written in the form

aN = v dq dt

where q is the angle of the velocity vector. Thus, the normal component of acceleration can also be interpreted to be a measure of how fast the direction of the velocity vector is changing.

Moreover, (6) also allows us to develop another formula for k. In particular, since v is parallel to T, we have

v×a =  dv dt ( v×T)+kv2( v×N) = kv2( v×N)

Since v and N are orthogonal, it follows that || v×N|| = v·1·sin( p/2) = v, so that

|| v×a|| = kv2|| v×N|| = kv3

Finally, solving for k yields another means of computing curvature:

k = || v×a|| v3

(7)

EXAMPLE 4    Find the linear acceleration and curvature of the helix

r( t) = á 3cos( t) ,3sin(t) ,4t ñ

Solution: The velocity and acceleration are, respectively, given by

v( t) = á -3sin( t) ,3cos(t) ,4 ñ ,        a = á -3cos(t) ,-3sin( t) ,0 ñ

It follows that the speed is given by

v = 9sin2( t) +9cos2( t) +16  = 5

so that the linear acceleration is given by

dv dt  =  d dt 5 = 0

To compute the curvature, we first compute v×a :

v×a  =  á -3sin( t) ,3cos(t) ,4 ñ × á -3cos( t) ,-3sin( t) ,0 ñ  =  á 12sint,-12cost,9 ñ

Thus, (7) implies that the curvature is

k = 144sin2( t) +144cos2( t)+81 53  =  3 25

       

EXAMPLE 5    Find the curvature of the vector-valued function

r( t) = á sinh( t) ,t,cosh( t) ñ

Solution: The velocity is v( t) = ácosh( t) ,1,sinh( t) ñ , so that the speed is

v =  cosh2( t) +1+sinh2( t)  =  2cosh2( t)  = Ö2cosh( t)

As a result, the linear acceleration is

dv dt  =  d dt Ö2cosh( t) = Ö2sinh( t)

The derivative of v( t) then yields the acceleration,

a( t) = á sinh( t) ,0,cosh( t) ñ

and the cross-product v×a is then given by

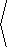
v×a = ê ê ê 1 sinh( t) 0 cosh( t) ê ê ê , ê ê ê sinh( t) cosh( t) cosh( t) sinh( t) ê ê ê , ê ê ê cosh( t) 1 sinh( t) 0 ê ê ê

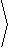
which via the identity cosh²( t) -sinh²( t) = 1 simplifies to

v×a = á cosh( t) ,-1,-sinh(t) ñ

Thus, (7) implies that the curvature is

k =   cosh2( t) +1+sinh2( t) 23/2cosh3( t)  =  2cosh2( t) 23/2cosh3( t)  =  1 4cosh2( t)

       

Check your Reading: Is k ever 0 in example 5?