Research Programs

 

Ultracold Neutrons at LANSCE

 

Ultracold neutrons (UCN) have kinetic energy below about 350 neV (nano-electron Volts), this corresponds to a velocity of \(\le 8\) m/s. At this energy the de Broglie wavelength of a UCN is approximately 50 nm or a few 100 times the distance between atoms in a solid. Because of this, UCN see a large collection of atoms when they interact with a material and coherently scatter from the surface. Although neutrons are electrically neutral they interact with the nuclei of atoms in a solid via the strong nuclear force. This fact allows UCN to stored in material bottles.

 

Two other forces of nature become important at UCN energy scales, gravity and magnetism. Since neutrons have mass they feel Earth's gravitational pull. For most neutron physics experiments, where neutrons are travel a few to tens of meters at 2200 m/s, the deflection due to gravity can almost be ignored. UCN, however, only have enough kinetic energy to rise about 3 m in Earth's gravity (\(m_n g = 100\) neV/m). If one were to make a bucket of the right material and about 2 to 3 m tall, they could store UCN in the bucket with no lid. Neutrons interact with magnetic fields through their spin or magnetic moment and experience a potential of \(V_B = - \vec{\mu}_n \cdot \vec{B} \). The magnetic potential is approximately 60 neV/T, but it is a spin direction dependent potential. UCN with spins aligned with the field will lose energy and those with opposite spin orientation will gain energy. Therefore a magnet with a sufficiently high field can be used to polarize UCN.

 

Around the world UCN are used in experiments that are investigating everything from the structure of the Standard Model of Particle Physics to the origin of the matter vs anti-matter asymmetry in the universe. Below are descriptions of experiments that I am currently collaborating on or have collaborated on in past.

 

The video below shows UCN being loaded into a stainless steel bottle and emptied into a \(^3\)He neutron gas counter. Everytime the light blinks a neutron is being captured on \(^3\)He, creating ions that trigger the detector.

 

 

Publications :

 

Back to top

 

nEDM @ LANL

 

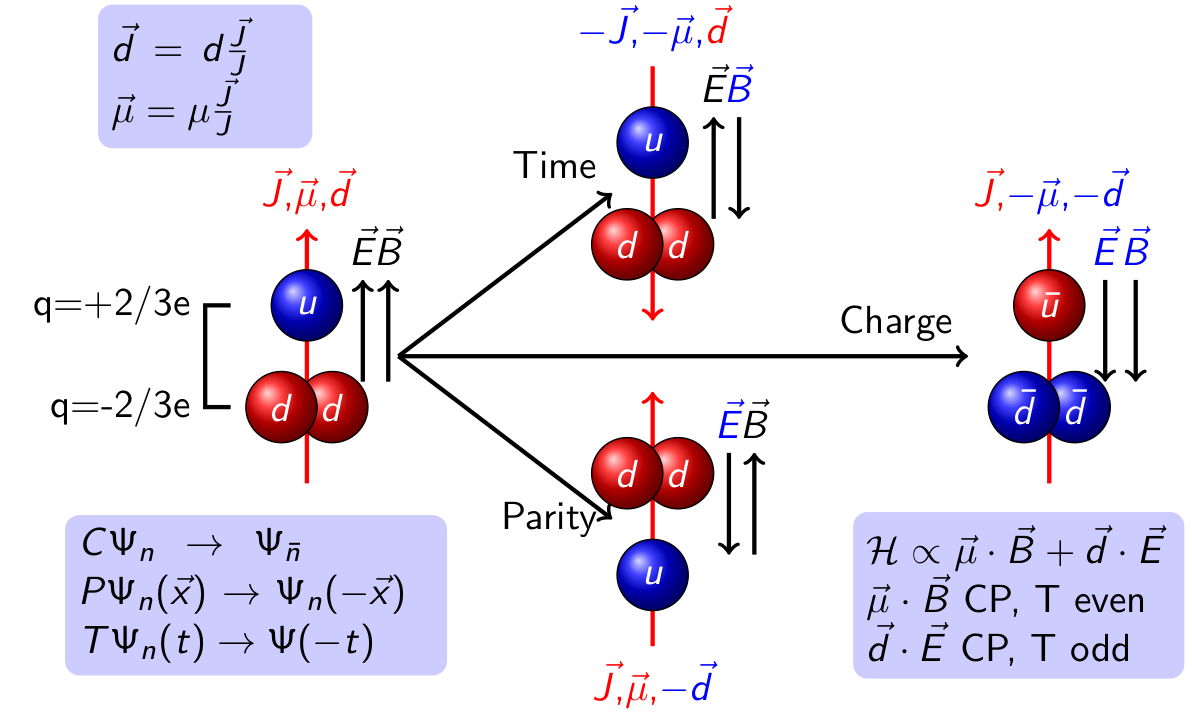
nEDM Prototype Members of the LANL nEDM collaboration in front of the prototype apparatus. (Top (left to right) : T. M. Ito (LANL), S. Clayton(LANL), R. Dadisman (UKy), B. Plaster (UKy), Bottom (left to right) : R.W. Pattie Jr. (ETSU), A. Aleksandrova (UKy), J. Long (IU))

 

One of the outstanding question in modern physics is, "How did the universe end up being uniformly dominated by matter, devoid of pockets or regions of antimatter?" If the big bang created equal amounts of matter and antimatter then some process must have violated this balance. In 1967, Andrei Sakharov proposed a set of conditions which must be fulfilled to violate the matter antimatter balance. One of the conditions is that the symmetries of Charge Conjugation \(C\) and Parity \(P\) are violated together. \(CP\)-violating processes have been discovered but are insufficient to explain the observed universe.

 

Its possible that neutrons can provide the answer. A permanent electric dipole moment in the neutron would be the result of \(CP\)-violating interactions. Current experimental sensivities are roughly six orders of magnitude away from the Standard Model prediction of the neutron's EDM. Meaning new theories or extensions to the Standard Model could exist that would create enough \(CP\)-violation to explain the matter asymmetry.

 

An electric dipole occurs when oppositely charged bodies are bound together at some fixed separation distance. The electric dipole moment (EDM) is a quantity defined by the product of the charge and the separation distance. In the neutron one could imagine at the average position of u-quark (+2/3 \(e^-\)) and the two d-quarks (-1/3 \(e^-\)) are slightly offset generating a very small EDM. Theoretical predictions suggest that for the neutron the EDM is \(d_n \approx 10^{-32} e \cdot\) cm. If the neutron was the size of the Earth this would correspond to a separation distance of the thickness of a human hair. Current experimental limits, however, are 6 orders of magnitude away from detecting an EDM at the predicted level. Extensions to the standard model predict large values for \(d_n\), so even if experiments can't reach the \(10^{-32} e\cdot\)cm sensitivity they can confirm or constrain new theories.

 

The Los Alamos room temperature neutron EDM experiment will improve the limits on \(d_n\) by a factor of 10 using Ramsey's Method of Separated Oscillatory Fields. This technique works by storing polarized neutrons in a region with uniform magnetic and electric fields applied. Typical the fields will be oriented so that they are aligned, with the ability to flip the direction of the electric field. A pulsed magnetic field is applied to tilt the neutron's spin by 90\(^\circ\) with respect to the fields, causing the neutrons to precess. At a later time another pulse is used to tilt the spins another 90\(^\circ\) to the opposite polarization from the beginning of this process. The neutrons are then emptied into a detector that can determine their polarization. The precession frequency is given by $$ \nu_0= \frac{-2}{h} ( \mu_n |B| \pm d_n |E|),$$ where\(h\) is Planck's constant, \(\mu_n\) is the neutrons magnetic moment, \(B\) and \(E\) are the field strenghts, and the \(\pm\) denotes whether the electric field is align/anti-aligned with the neutron spin. If \(d_n \neq 0\) the precession frequency would change when the electric field direction is flipped. This difference in precession frequency would cause the second pulse to be less efficient at tilting the neutron's spin resulting in a change of the measured polarization.

 

Publications

 

Back to top

 

UCNτ

 

A free neutron will decay into a proton, electron, and anti-electron neutrino \(n \to p+ e^- + \bar{\nu}_e \) in approximately 15 minutes. Currently there is a discrepancy between the two methods of measuring the neutrons lifetime, experiments using beams of cold neutrons and experiments using storaged UCN. Most of the storage measurements to date have use material walls to contain the UCN, which can cause unaccounted for losses and shorten the measured lifetime. The UCNτ experiment at Los Alamos was designed to combine a magneto-gravitational trap with in-situ counting to eliminate material interactions during storage.

 

 

Publications

 

Similar Experiments :

Back to top

 

UCNA

 

UCNA Spectrometer

 

The UCNA experiment measures the asymmetry in the emission direction of the electron with respect to the neutron spin in β-decay. The asymmetry, \(A\), is determined by confining polarized ultracold neutrons in the bore of a 1 T superconduction solenoidal magnet and counting the number of electrons emitted along the polarization direction versus against it, $$A_{exp} = \frac{N_e^\uparrow - N_e^\downarrow}{N_e^\uparrow + N_e^\downarrow} \sim A P \beta \cos (\theta), $$ where \(\beta\) is the electron's velocity, \(P\) is the average polarization, and \(\theta\) is the angle between the neutron's spin and the electron's emission direction. The parameter \( A\) is defined to first order in the standard model of particle physics as $$ A_0 = \frac{-2(\lambda^2-|\lambda|)}{(1+3\lambda^2)}, $$ where \( \lambda \equiv g_A / g_V \) the ratio of the axial-vector to vector coupling constants. The types of interactions that obey Lorentz invariance are the vector \(V \), axial vector \(A\), scalar \(S\), tensor \(T\), and pseudo-scalar \(P\) and current experimental evidence suggests the weak interaction is purely of the form \(V-A\). Precision measurements of angular correlations in \(\beta\)-decay will allow physicists to better understand the form of the weak force.

 

Publications :

 

Similar Experiments around the world :

 

Back to top

 

N-N̄

 

Details Soon...

 

Back to top

 

Neutron Physics in the US

 

Details Soon...

 

Back to top