Quoting from the introduction: "Welcome to the world of pure mathematics where geometries exist in many dimensions and numbers are bigger than infinity. It’s a world where objects take on strange configurations. And if you thought that parallel lines never meet, you’re in for a surprise."

"For over a decade, Bertrand Russell tried to find a certainty through mathematics by reducing it to logic. In his massive work, Principia Mathematica, it took him 362 pages to prove that one plus one equals two. Twenty years later, another mathematician, Kurt Godel, proved that mathematics would never be completely certain."

"Do the abstract objects of mathematics have anything to do with the real world? Is mathematics the key that unlocks the universe? ... Throughout history, mathematician believed in the certainty of mathematics, that every problem, no matter how difficult, had a solution. But over the last 50 years certain events have shaken this belief. Will there ever be solutions to these questions? Do the abstract problems of pure mathematics matter in the real world? Or are mathematicians in a world of their own?"

Bertrand Russell and Principia Mathematica Kurt Godel Fermat's Last Theorem The Goldbach Conjecture The Riemann Hypothesis Classification Problem for 4-D manifolds "P not equal to NP" Problem Invariant Subspace Problem for Hilbert Spaces Jean Dieudonne Michael Atiyah Greg Moore

1. Proof Beyond Doubt

Isaac Newton Proof Arithmetic, Geometry, Analysis "Numbers are the fabric of mathematics." Prime numbers Euclid proves there are an infinite number of primes. Twin primes The Goldbach Conjecture. All even numbers are the sum of two primes. Merten's Conjecture (false) Fermat's Last Theorem Rene Thom Paul Erdos

2. The Foundations of Mathematics

Aristotle Euclid and The Elements Non-Euclidean geometries Klein bottle Dimensions "Time is an example of the fourth dimension."

3. Discovery or Invention

Platonism (mathematical objects are "real") The Golden Rectangle Symmetry in nature Group theory and Galois

4. A Question of Infinity

Irrational numbers π Mersenne primes (2n-1) Raymond Smullyan George Cantor and cardinality Different infinities (alephs)

5. Cracks in the Foundation

Gottlieb Frege Bertrand Russell Russell's Paradox: catalogues and metacatalogues Alfred North Whitehead Principia Mathematica Ivor Grattan-Guiness

6. Back to Basics

Nicholas Bourbaki David Hilbert "He hoped by taking the meaning out of mathematics... he would free it once and for all from paradox and contradiction."

7. The Uncertain Future

Kurt Godel Godel's Incompleteness Theorem (no complete system of axioms is complete) Continuum Hypothesis Symbolic logic and computers The 4-Color Problem "We are not simply, as mathematicians, in the business to get answers, we want to understand." "Mathematics has lead to the most certain body of knowledge we have."

Pierre de Fermat (1601-1665)	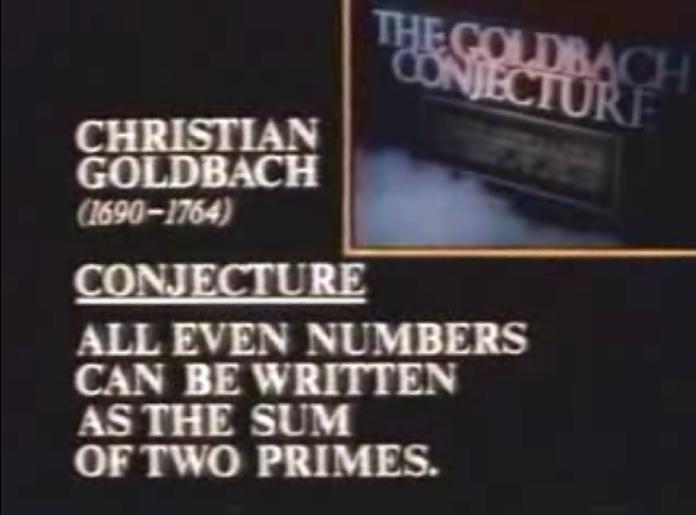The Goldbach Conjecture
Non-Euclidean Triangles	The Logic of a Proof
Evariste Galois (1811-1832)	"1 + 1 = 2" in Principia Mathematica

A Mathematical Mystery Tour first aired when I (Bob Gardner) was in my first year of graduate school at Auburn University in the Math Department. It was great timing and I definitely benefited from exposure to this show. In my opinion, it is still the best popular level program covering what pure mathematics is and how it is done. It gives a bit of history, some philosophy, and mentions several very deep mathematical ideas (such as Russell's Paradox and the Continuum Hypothesis). I try to expose all of the ETSU math graduate students to this program at some point during their time at ETSU.

I have shown it in some of my classes. An outline of the show is posted online here. This was posted for my Foundations and Structure of Mathematics 1 fall 2004 class. This graduate level class was aimed at elementary and middle school math teachers. I also try to show the section "Cracks in the Foundation" in my senior level Analysis 1 class. We discuss Russell's paradox in the class, so this part of the show fits well with the classroom material.

On the negative side, the show makes claims concerning the "golden rectangle" and "golden section" which are a bit misleading. A nice discussion of the golden section which goes into details on its use in architecture can be found in The Golden Ratio - The Story of Phi, the World's Most Astonishing Number by Mario Livio, New York: Broadway Books (2002). There is also an implication that Evariste Galois wrote down his mathematical ideas in a hurry the night before he died in a duel and that this was the extent of his work. Details on this bit of history are spelled out in The Equation That Couldn't Be Solved by Mario Livio, New York: Simon & Schuster (2005).

Some parts of the show are dated. There is much discussion of "Fermat's Last Theorem" and the fact that it is (in 1985) an unsolved conjecture. The complete absence of female mathematicians in A Mathematical Mystery Tour is striking by today's standards! The only females in the show are students in the Stuyvesant High School classroom where Raymond Smullyan is lecturing - and none of them have a speaking role!

1. The Language of the Universe
2. The Genius of the East
3. The Frontiers of Space
4. To Infinity and Beyond

Return to Bob Gardner's webpage

Last updated: February 10, 2010