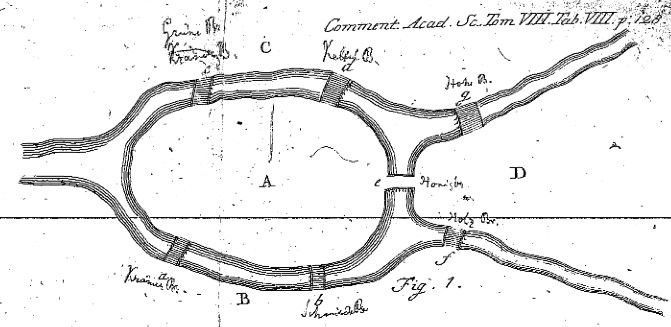
 Konigsberg Bridge |
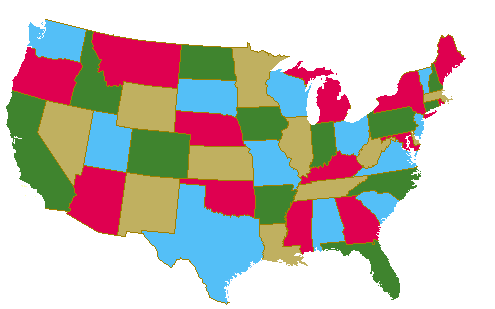 A Four Coloring of a Map |
 Konigsberg Bridge |
 A Four Coloring of a Map |
COURSE NUMBER: MATH 5450
TIME: 3:45-5:05 TR, PLACE: Online through Zoom CALL# 13372
INSTRUCTOR: Robert "Dr. Bob" Gardner; OFFICE: Room 308F of Gilbreath Hall
OFFICE HOURS: By appointment; PHONE: 439-6979 (Math Office 439-4349)
E-MAIL: gardnerr@etsu.edu
WEBPAGE: www.etsu.edu/math/gardner/gardner.htm.
TEXT: Graph Theory by J. A. Bondy and U. S. R. Murty, Graduate Texts in Mathematics 244 (Springer, 2008). For material on algebraic graph theory, we will turn to the supplemental reference Algebraic Graph Theory by Chris Godsil and Gordon Royle, Graduate Texts in Mathematics 207 (Springer, 2001). For material on topological graph theory, we will turn to the supplemental reference Graphs on Surfaces by Bojan Mohar and Carsten Thomassen, Johns Hopkins Studies in the Mathematical Sciences (Baltimore: Johns Hopkins University Press, 2001). More details are on the supplemental references is below.

PREREQUISITE: Graph Theory 1 (MATH 5340).
DESIRE2LEARN: I will not rely on the Desire2Learn ("D2L") website. Instead, I will simply post all material directly on the internet. However, I will post your grades on D2L and there will be links to the recordings of the lectures.
CLASS NOTES: We will use digital notes for the presentation of definitions, examples, and proofs of some theorems. Limited marginal notes, additional examples, and further explanations will be given using handwritten notes and a document camera. Copies of the notes are online. You should read the online notes to be covered in class before each class (we may not have class time to cover every little detail in the online notes). Try to understand the definitions, the examples, and the meanings of the theorems. After each class, you should read the section of the book covered in that class, paying particular attention to examples and proofs.
ABOUT THE COURSE: Graph theory is a relatively new area of math. It lies in the general area of "discrete math" (as opposed to continuous math, such as analysis and topology), along with design theory and coding theory. Historically, it is motivated by applied problems and still finds numerous applications, particularly in computer science (such as network design and the efficiency of algorithms). However, today it is a very vibrant area of pure mathematical research. ETSU has had a number of research graph theorists over the past several years, including Drs. Lawson, D. Knisley, Boland, Haynes, and Beeler. In this class we will survey graph theory. Homework assignments will mostly involve the standard exercises in the text book, but will occasionally involve more advanced exercises. Some emphasis will be put on the research of those current ETSU faculty members involved in areas related to graph theory. In particular, some lectures will deal with graph (and digraph) decompositions, coverings, and packings. Automorphisms of graph (and digraph) decompositions will also be explored. We may have a few guest lectures given by my departmental colleagues on their area of research.
OUTLINE:
Our tentative (and ambitious) outline is as follows (we may also cover some other topics from the text book or elsewhere, like topics from algebraic graph theory and topological graph theory; see the Supplemental References below):
Chapter 4. Trees: Tree, forest, path connectedness of trees, leaf, rooted tree, branching, reachable vertices, median order, subtrees, spanning trees, classification of bipartite graphs, Cayley's Formula, number of spanning trees, cotree, fundamental cycle, even subgraphs, fundamental bonds, cyclomatic number.
Chapter 5. Nonseparable Graphs: Cut vertex, separation of a connected graph, nonseparable graph, block of a graph, ear of a graph, nested sequence of graphs, ear decomposition, directed ear, directed ear decomposition, feedback arc set of a digraph, fundamental cycle of a digraph.
Chapter 13. The Probabilistic Method: Random graphs, probability space, events, probability, random variable, dependent/independent random variables, expectation of a random variable, linearity of expectation, crossing number, "almost surely," Markov's Inequality, variance, Chebyshev's Inequality, stability numbers of random graphs, threshold functions, balanced graph, the Local Lemma, two colorable hypergraphs, even cycles in digraphs.
Chapter 9. Connectivity: Vertex connectivity, local connectivty, vertex cuts, the Fan Lemma, edge connectivity, essentail edge connectivity, connectivity in digraphs, three-connected graphs, contractions and expansions of three-connected graphs, submodularity, edge connectivity of vertex-transitive graphs, the Nash-Williams Orientation Theorem, Gomory-Hu trees and edge connectivity, chordal graphs, clique cuts, simplicial vertices, tree representations of chordal graphs.
Chapter 10. Planar Graphs: Planar/nonplanar graph, points and lines of a planar embedding, curve, closed curve, simple curve, Jordan Curve Theorem, interior/exterior of a simple closed curve, subdivision of a graph, stereographic projection, face of a graph, outer face, boundary of a face, homeomorphism of the plane, degree of a face, subdivide a face, dual of a graph, plane dual, plane triangulation, maximal planar graph, directed planar dual, vector spaces and duality, Euler's formulat concerning vertices/edges/faces or a planar graph, bridge, k-bridge, unique plan embeddings, Kuratowski's Theorem (classifying planar graphs in terms of subgraphs), minor of a graph, Kuratowski minor, convex embedding, surface, Mobius band, orientable/nonorientable surface, double torus, projective plane, classification theorem for surfaces, Euler characteristic of a surface, circular embedding.
Chapter 11. The Four-Colour Problem: Four-Colour Problem/Conjecture (face, vertex, edge versions), k-face colouring, Appel and Haken's proof of the Four-Colour Theorem, k-vertex-colouring, k-edge-colouring, Five-Colour Theorem.
GRADES: Since this is an online class, your grade will be determined by the average on the assigned homework exercises. Grades will be assigned based on a 10 point scale with "plus" and "minus" grades being assigned on a 3 point subscale (for example, a 90, 91, 92 is an A-).
HOMEWORK: Homework will be assigned and collected at roughly one week intervals. YOU MUST SHOW ALL DETAILS ON THE HOMEWORK PROBLEMS!!! Justify every step and claim you make - this is how you convince me that you know what you are doing. You may find some answers online, but these rarely sufficiently justify all steps and are unacceptable as homework solutions.
ACADEMIC MISCONDUCT: While I suspect that you may work with each other on the homework problems (in fact, I encourage you to), I expect that the work you turn in is your own and that you understand it. Some of the homework problems are fairly standard for this class, and you may find proofs online or in an online version of the solutions manual. The online proofs may not be done with the notation, definitions, and specific methods which we are developing and, therefore, are not acceptable for this class. If I get homework from two (or more) of you that is virtually identical, then neither of you will get any credit. If you copy homework solutions from an online source, then you will get no credit. These are examples of plagiarism and I will have to act on this as spelled out on ETSU's "Academic Integrity @ ETSU" webpage (last accessed 7/22/2020). To avoid this, do not copy homework and turn it in as your own!!! Even if you collaborate with someone, if you write the homework problems out in such a way that you understand all of the little steps and details, then it will be unique and your own work. If your homework is identical to one of your classmates, with the exception of using different symbols/variables and changing "hence" to "therefore," then we have a problem! If you copy a solution from a solution manual or from a website, then we have a problem! I will not hesitate to charge you with academic misconduct under these conditions.
SUPPLEMENTAL REFERENCES:

SYLLABUS ATTACHMENT: You can find an on-line version of the university's syllabus attachment (which contains general information concerning advisement, honor codes, dropping, etc.; last accessed 1/5/2021).
IMPORTANT DATES: (see the official ETSU calendar for more details; accessed 1/5/2021):
| |
|
||||
5.2. Separations and Blocks |
5.2.2(a) |
||||
13.1.2(b) |
|||||
13.2.7(b) |
|||||
10.2. Duality |
10.2.4 |
||||
10.3. Euler's Formula |
10.3.1, 10.3.2(a), 10.3.2(b) |
||||
Return to Dr. Bob's webpage
Last updated: April 19, 2021.